
이번에 알아볼 것은 그래프 탐색의 대표적인 방법인
그래프의 표현 방법인 인접 리스트와 인접 행렬입니다.
그래프와 트리에 관한 내용은 이전 포스팅을 참고해주세요.
https://uknowblog.tistory.com/357
[자료구조] 그래프(Graph)와 트리(Tree) - 점과 선의 예술
그래프(Graph) 그래프란 무엇일까요? 점과 선이요. 가장 간단하면서 가장 잘 나타낸 말인 것 같습니다. 이산 수학과 컴퓨터 공학에서 말하는 그래프는 각각의 정점(Node, Vertex)이 간선(Edge)으로 이어
uknowblog.tistory.com
그래프의 연결 표현 : 인접 배열과 인접 리스트
그래프의 연결을 표현하는 방법에는 인접 배열과 인접 리스트가 있습니다.
이름처럼 배열을 썼느냐, 리스트를 썼느냐의 차이입니다.
인접 행렬(Adjacency Martix)


인접 행렬은 각 배열의 연결관계를 0과 1로 나타낸 방법입니다.
n * n 배열로 나타내며,
arr[1][2] = 1 일 경우, 1에서 2로 가는 경로가 존재함을 의미합니다.
가중치가 없을 경우, 1과 0으로 표현하기에 Boolean 자료형을 사용해 true, false로 나타낼 수도 있습니다.

양방향 그래프의 경우, 대각선을 기준 으로 대칭을 이룹니다.
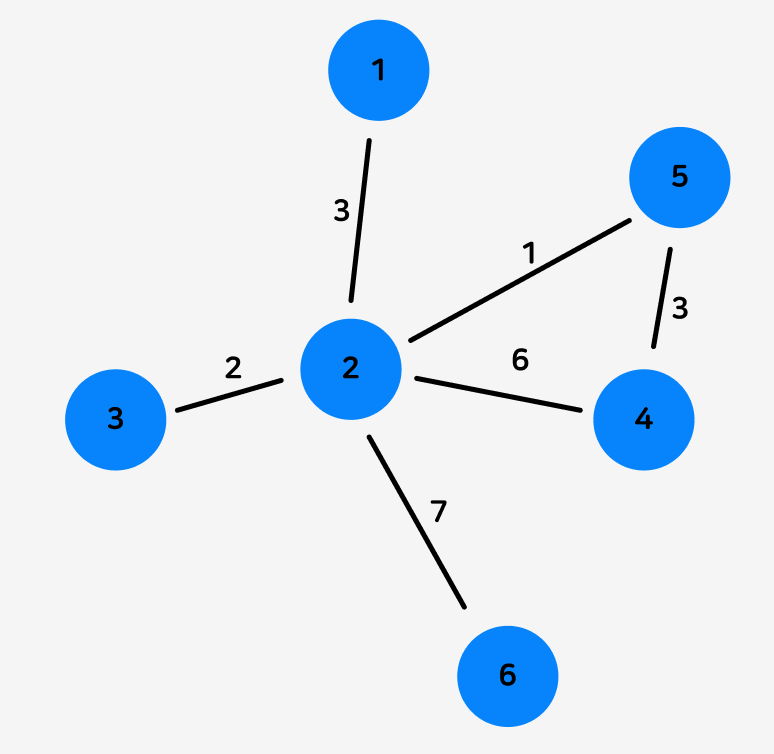
방향을 가진 그래프의 경우
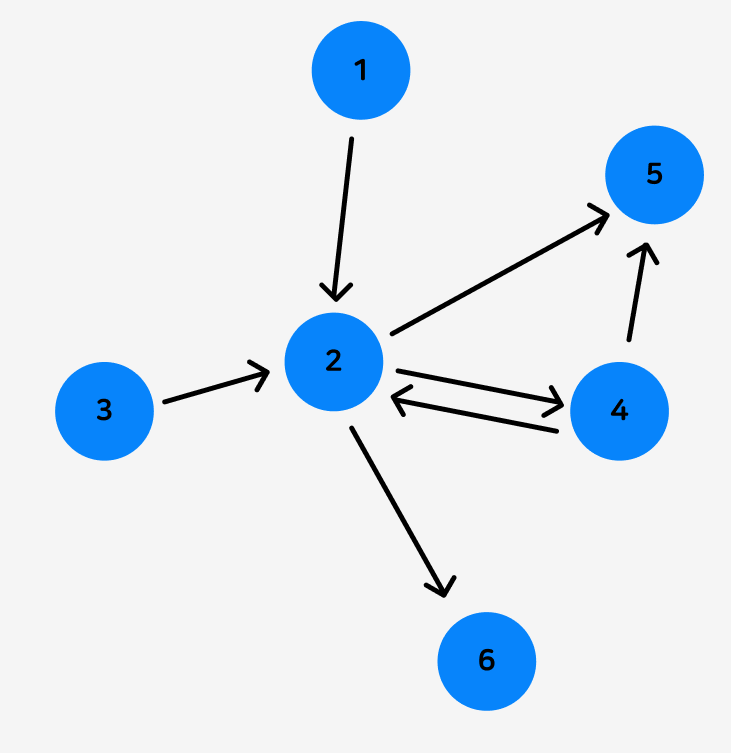
방향을 가진 그래프의 경우, 위와 같이 나타낼 수 있으며,
대각선을 기준으로 대칭을 이루지는 않습니다.
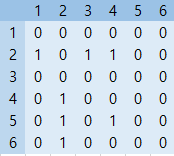
가중치를 가진 그래프의 경우
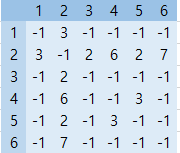
가중치를 가진 그래프의 경우, 갈 수 있을 경우 해당 노드에서 다른 노드로 가는 가중치 설정합니다.
arr[3][2] = 2 일 경우, 3번 노드에서 2번 노드로 가는 비용(가중치)가 2임을 의미합니다.
갈 수 없을 경우 -1 혹은 0 으로 두며,
-1, 0 둘 중 무엇을 사용할지는 개발자의 성향이나 상황에 따라 다릅니다.
인접 리스트 (Adjacency List)
인접 행렬이 각 노드의 연결을 배열로 나타냈다면,
인접 리스트는 각 노드의 연결을 리스트(List)로 나타낸 형태입니다.

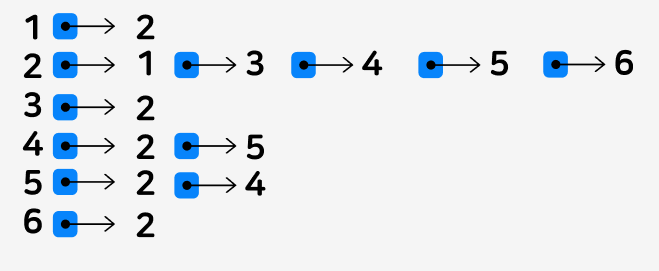
이를 코드로 나타내면 아래와 같습니다.
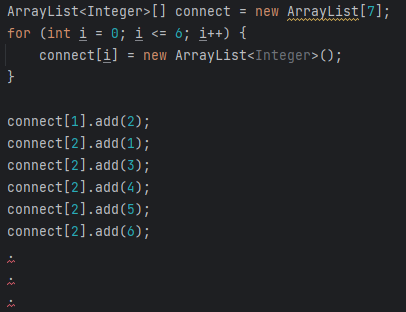
ArrayList<Integer> 배열을 만들고,
1번 노드에 연결된 노드 2번 추가,
2번 노드에 연결된 노드 1번 추가, 3번 추가, 4번 추가, 5번 추가, 6번 추가
.
.
.
와 같이 List를 통해 한 노드와 연결된 다른 노드를 표현합니다.
인접 행렬 vs 인접 리스트
그럼 인접 행렬과 인접 리스트 중 뭐가 좋을까요?
다들 예상했던 답변이겠지만
'때에 따라 다릅니다'
인접 행렬의 경우

인접 행렬의 경우, 1번 노드와 2번 노드의 연결 여부를 확인하려면 단순히 arr[1][2]를 확인하면 됩니다.
시간복잡도로 표현하자면, 연결여부 확인 자체에는 O(1) 밖에 되지 않습니다.
하지만, 한 노드와 연결된 다른 노드를 찾는 것이라면 이야기가 달라집니다.
예를 들어, 2번 노드와 연결된 다른 노드를 찾아야 한다면
arr[2][0], arr[2][1], arr[2][3], arr[2][4], arr[2][5], arr[2][6]을 모두 뒤져봐야 합니다.
즉, 연결된 다른 노드를 찾는데에는 O(n)이 소모됩니다.
또, 그래프의 연결 여부와 관계없이 행렬을 통해 표현하기 때문에 항상 n * n 의 배열이 필요하므로,
차지하는 메모리 역시 인접 리스트에 비해 큽니다.
그래프의 크기가 커질수록 이는 꽤나 부담스러워 질 수 밖에 없죠.
인접 리스트의 경우

반면 인접 리스트는 인접한 정점들의 리스트만 저장합니다.
늘 n * n의 배열이 필요한 인접 행렬에 비해 메모리를 효율적으로 사용할 수 있습니다.
인접 행렬을 통해 구현했다가, 메모리가 초과하여 인접 리스트로 바꾼 적도 꽤나 있습니다.
다만, 한 노드에서 다른 노드로 가는 간선의 존재 유무를 확인하려면 해당 정점과 연결된 노드의 개수, 즉 차수(Degree) 만큼 소요됩니다.
O(degree)인 셈이죠. 간선의 개수가 많아질 수록 O(1)이던 인접 행렬에 비해 더 낮은 퍼포먼스를 보일 수 있습니다.
반면, 두 노드간의 간선의 존재 유무가 아닌,
한 노드에서 연결된 다른 노드들을 찾는 것이 목적이라면 인접행렬에 비해 빠르게 알아낼 수 있습니다.
정리
인접 행렬은 간선의 존재 여부를 빠르게 확인하는데 특화되어 있습니다.
arr[1][2] 와 같이 접근하면 되니까요. 때문에 O(1)의 시간이 소요됩니다.
하지만 늘 n * n 배열을 필요로 하므로, 그래프의 노드 개수가 많아질 수록 부담스러울 수 있습니다.
반면에 인접 리스트는 더 효율적인 메모리 관리가 가능합니다.
노드의 수에 비해 간선의 수가 적을수록 더욱 더 유용하지요.
하지만 간선의 존재 여부를 확인하는데 평균적으로 O(degree) (degree는 차수) 시간이 소요됩니다.
간선이 많으면 많을 수록 오히려 더 많은 메모리를 사용할 수도 있지요.
간선의 존재 유뮤 확인이 아닌, 한 노드와 연결된 다른 노드를 찾는게 목적이라면,
인접리스트가 인접행렬에 비해 더 빠를 수 있습니다.
노드가 6개 있고, 2번 노드에 연결된 노드를 찾는다고 했을 때,
인접행렬은 arr[2][1], arr[2][3], arr[2][4], arr[2][5], arr[2][6] 모두 봐야 하지만,
인접리스트의 경우는 리스트이기 때문에, 그저 리스트 내 원소를 확인하면 되니까요.
모든 상황에 적합한 자료구조는 없으며,
때에 따라 적절한 방식을 택하면 됩니다.
'CS 지식 > 자료구조' 카테고리의 다른 글
| [자료구조] 스택, 큐, 데크 - 자료구조 삼대장 (0) | 2023.07.15 |
|---|---|
| [자료구조] 그래프(Graph)와 트리(Tree) - 점과 선의 예술 (1) | 2023.07.11 |
| [자료구조] 분리 집합(Disjoint set)과 유니온 - 파인드(Union-Find) (0) | 2022.11.04 |
