
1. 그래프(Graph)
그래프란 무엇일까요?
점과 선이요.
가장 간단하면서 가장 잘 나타낸 말인 것 같습니다.
이산 수학과 컴퓨터 공학에서 말하는 그래프는
각각의 정점(Node, Vertex)이 간선(Edge)으로 이어진 형태입니다.
1.1. 그래프의 시초


위 두 개의 그림은 다들 수학시간때 한 번씩 본 그림일텐데요.
'쾨니히스베르크 다리 건너기' 문제입니다.
쾨니히스베르크(현 러시아 칼리닌그라드) 중앙에는 섬이 있는데,
7개의 다리를 단 한 번씩만 모두 건널 수 있느냐? 라는 문제입니다.
이걸 단순화 시킨게 아래의 그림인데,
각 육지를 점, 다리를 선으로 나타낸 것이 그래프의 시초 중 하나라고 추측되고 있습니다.
참고로 위 문제는 '한 번씩 모두 건널 수 없다'라는 것이 수학적으로 증명되었으며,
자세한 내용은 오일러 정리 혹은 오일러 정리를 검색해보세요.
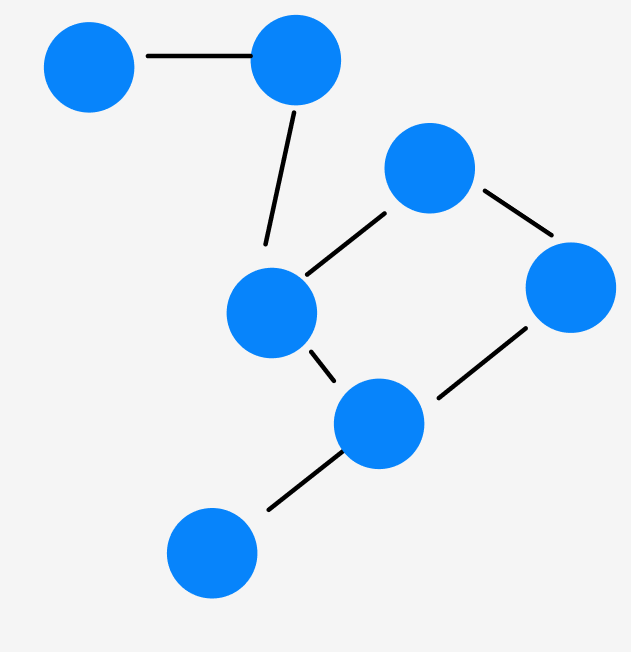
각 점들은 정점, Node, Vertex라고 하며,
선들은 간선, Edge 라고 부릅니다,
이들 정점과 간선으로 이루어진 세계가 그래프인 것이죠.
1.2. 그래프와 방향
1.2.1. 방향 그래프 (Directed Graph)
그래프는 방향을 가질 수도, 가지지 않을 수도 있습니다.
그래프가 방향을 가진다는 것은 일방통행을 의미합니다.
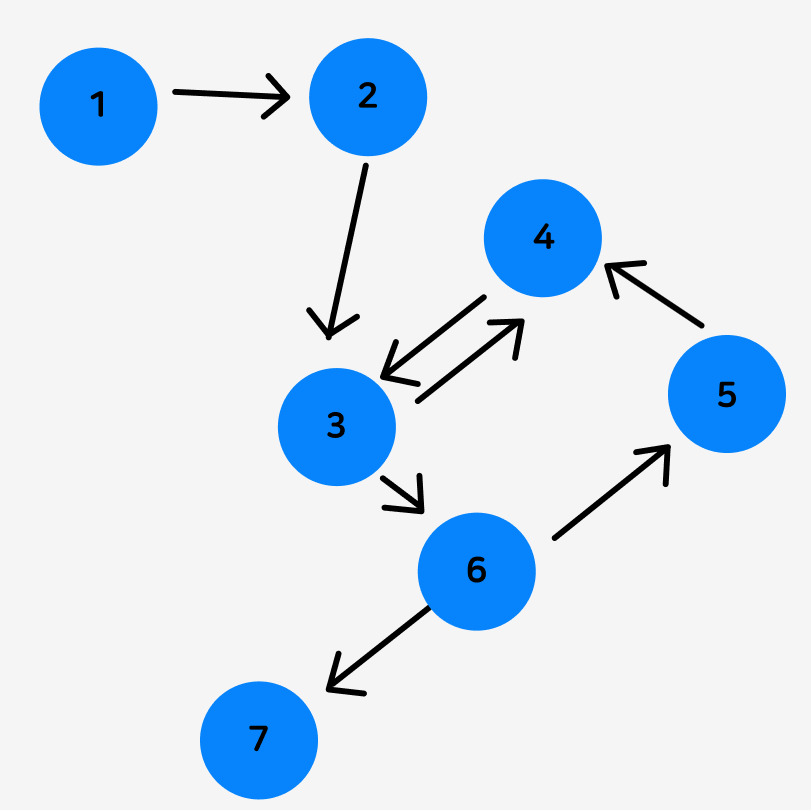
1번에서 2번으로 이동이 가능하나, 2번에서 1번으로는 이동이 불가능합니다.
5번에서 4번으로 이동은 가능하나, 4번에서 5번으로 바로 가는 경로는 없고,
4 -> 3 -> 6 -> 5로 4번 노드에서 5번 노드로 이동해야 합니다.
다만, 3번, 4번 노드와 같이 방향 그래프라 하더라도
서로간에 일방통행 간선이 있을 경우, 서로간의 직접적인 이동이 가능합니다.
1.2.2. 무방향 그래프 (Undirected Graph) / 양방향 그래프 (Bidirectional Graph)
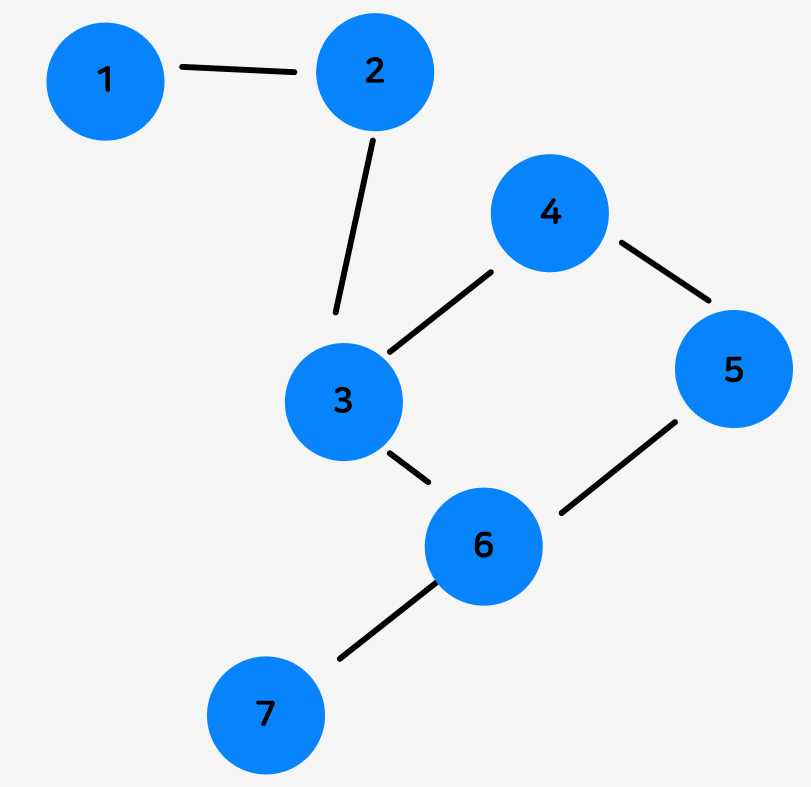
반면 무방향 그래프는 방향을 가지지 않는 그래프입니다.일방통행이 아니며, 서로 연결되어 있는 노드간의 상호 이동이 가능합니다.
때문에, 양방향 그래프라고도 하며,
코딩테스트 등에서는 특수한 경우가 아닌 이상 무방향과 양방향의 의미적 차이를 두지는 않는 듯 합니다.
1.3. 그래프와 가중치
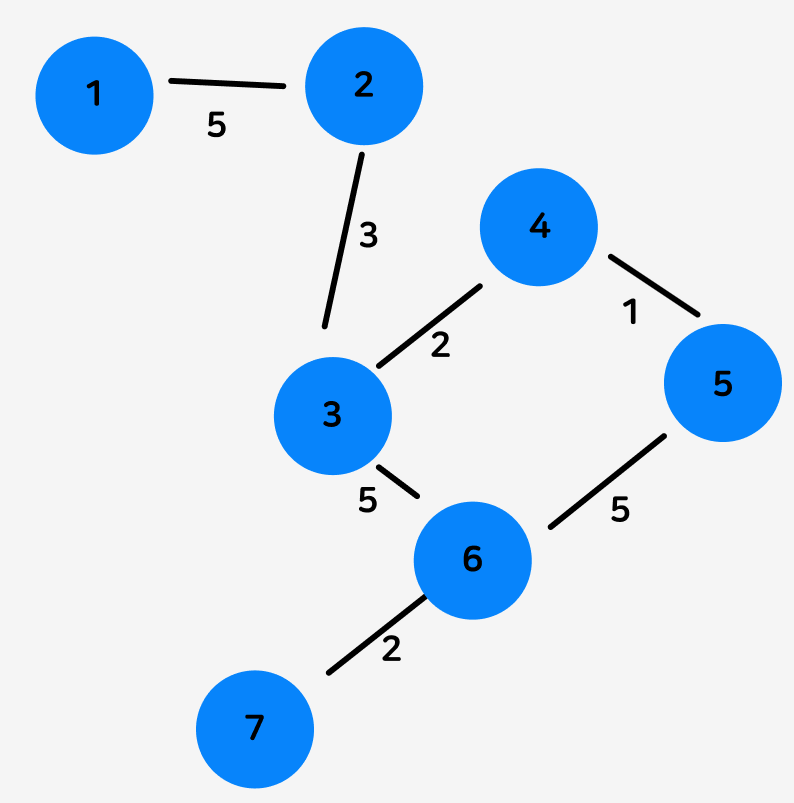
그래프의 간선은 가중치를 가질 수도 있습니다.
가중치란, 한 노드에서 다른 노드로 가는 비용입니다.
weight, cost 등으로 표현하곤 합니다.
1번 노드에서 2번 노드로 가기 위해서는 5의 비용이 필요하며,
1번 노드에서 3번 노드로 가려면 1->2->3, 8의 비용이 필요합니다.
이는 현실 세계에서 도시와 도로로 자주 비유되곤 합니다.
한 도시에서 다른 도시로 가는 거리, 시간, 비용(기름값) 등으로 생각할 수 있지요.
서울 <-> 수원
성남 <-> 용인
인천 <-> 안산 등
한 도시(노드)에서 다른 도시로 가는 경로가 있다고, 무조건 다 같은 거리, 시간, 비용이 드는 것은 아닙니다.
때문에 도시와 도로의 경우 가중치를 가지는 그래프가 주로 쓰이곤 합니다.
1번 노드에서 5번 노드로 가는 경로는 여러개인데요.
1->2(5)->3(8)->4(10)->5(11)
1->2(5)->3(8)->6(13)->5(18)
거치는 노드 수는 동일하나, 비용은 전자의 경우가 더 적은 것을 알 수 있습니다.
당연하게도, 비용(가중치)를 가지는 그래프의 경우
한 노드에서 다른 노드로 갈 때, 거치는 노드 수가 적다고 비용이 더 적게 드는 것은 아닙니다.
한 노드에서 다른 노드로 가는 최단 경로 혹은 최단 비용의 관한 문제는
다익스트라 알고리즘, 플로이드-워셜 알고리즘을 참고해주세요.
또한, 현실 세계에서 흔한 편은 아니지만, 간선지가 음수인 그래프도 있습니다.
SF 영화의 타임머신이 개발된다면, 한 도시에서 다른 도시로 가는 시간이 음수가 될 수도 있겠죠.
해당 경우의 최단 경로는 벨만-포드 알고리즘을 참고해주세요.
2. 트리(Tree)
트리는 그래프의 형태 중 하나입니다.
사이클이 없는 그래프를 의미하지요.
그럼, 사이클이란 뭘까요?
2.1. 사이클(Cycle)
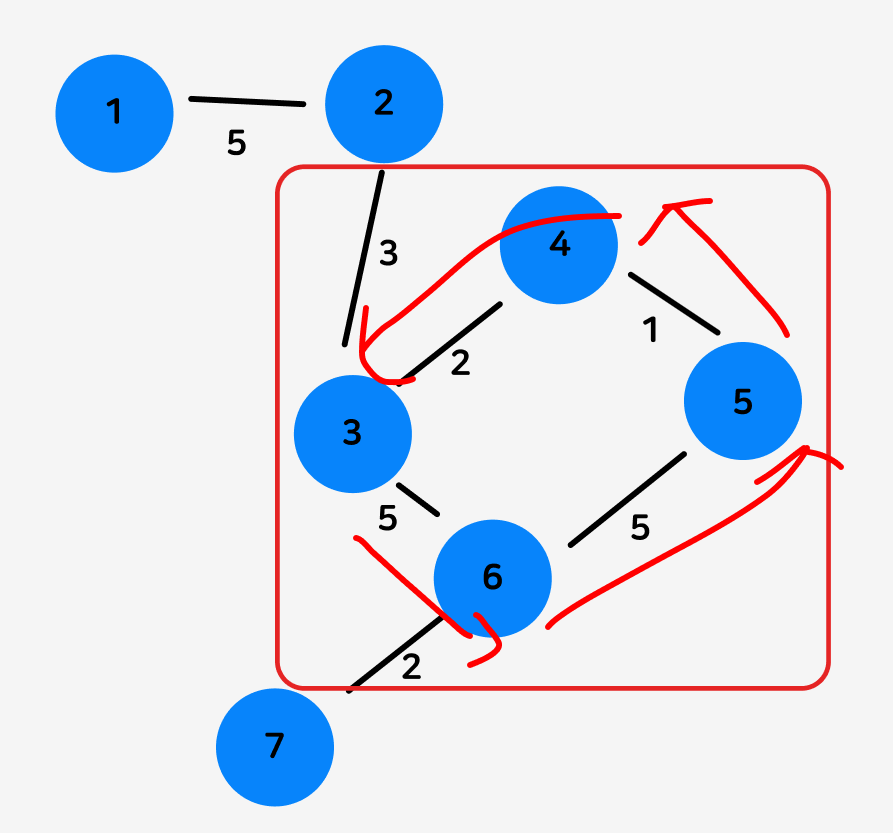
3->6->5->4->3으로, 다시 현재 노드로 돌아올 수 있습니다. 순환 구조를 띄는 것이죠.
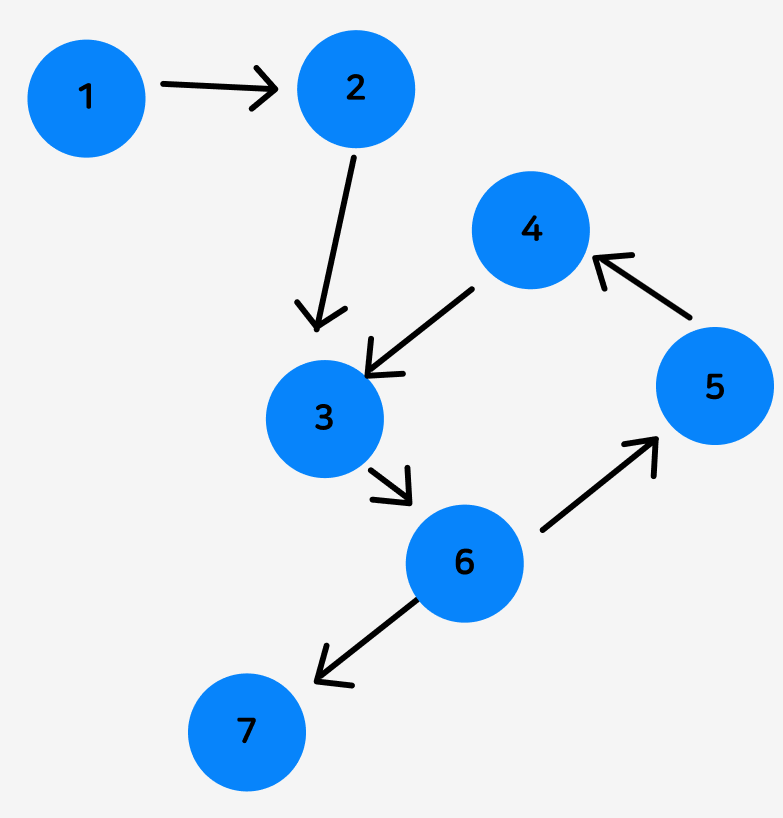
물론 방향 그래프에서도 사이클이 존재할 수 있습니다.
3 -> 6 -> 5 -> 4로 자기 자신으로 바로 돌아오는 경로가 있지요.
2.2. 사이클이 없는 그래프, 트리
이러한 순환구조(사이클)이 없는 구조를 트리(Tree) 라고 합니다.

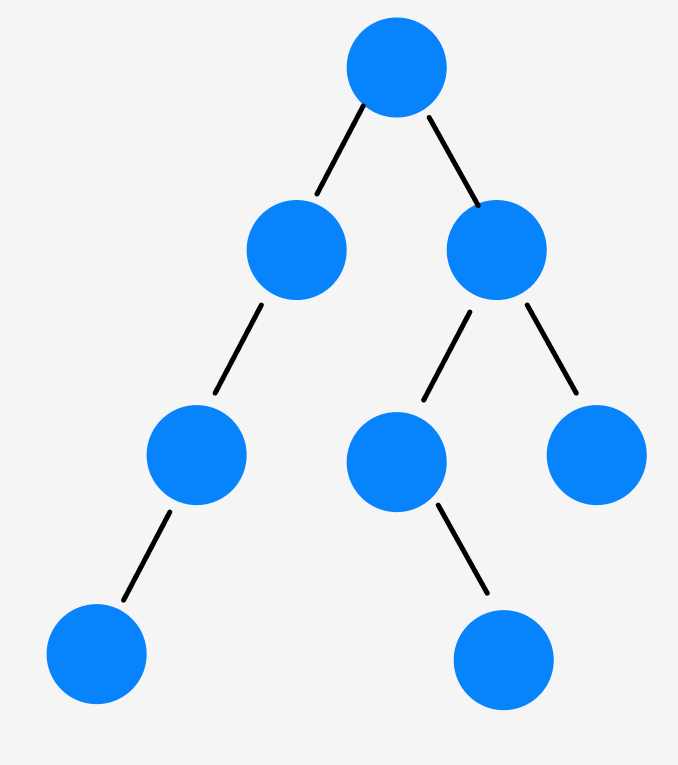
트리(Tree)라는 이름처럼,
나뭇가지는 뻗어나가 서로 이어지지 않듯이,
한 노드에서 다른 노드로 뻗어나가 서로 어이지지 않습니다.
나무를 거꾸로 뒤집어놓은 듯한 모습이죠.

??? : 엥 근데 서로 이어진 나무도 있지 않나요?
잠시 머리속에서 지워두세요.
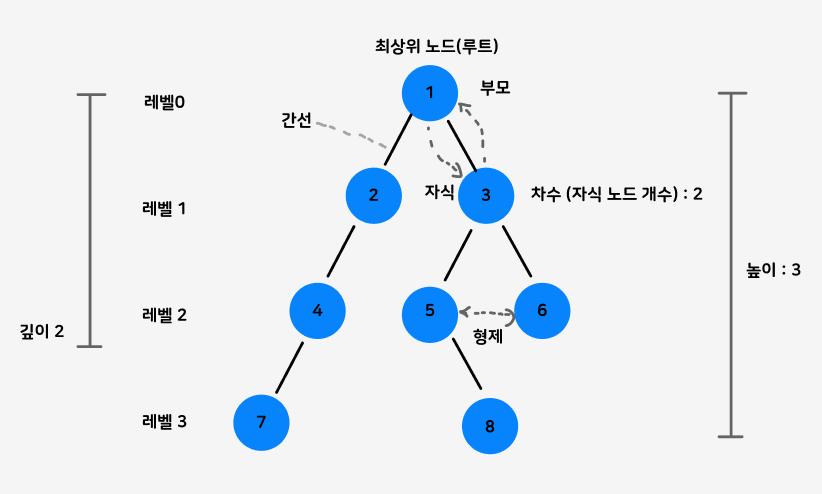
트리는 가장 위에 있는 노드, 즉 최상위 노드를 루트(root)라고 합니다.
그리고 바로 아래 노드를 자식 노드,
자식노드의 바로 위 노드를 부모 노드라고 합니다.
자식의 개수는 차수라고 하며,
3번 노드의 경우 5, 6번 노드 두 개의 자식 노드를 갖고 있기에 3번 노드의 차수는 2 입니다.
각 노드가 루트(최상위 노드)와 얼마나 떨어져 있는지를 깊이라고 하며,
같은 깊이를 가진 노드들을 묶어 레벨이라 합니다.
같은 레벨의 노드 끼리는 형제 노드라고 하지요.
최상위 노드와 가장 멀리 떨어져있는, 즉 가장 높은 레벨을 트리의 높이라 합니다.
폴더 구조 등도 트리의 한 예라 볼 수 있습니다.
목차 역시 마찬가지지요.
3. 후기
사실 그래프 탐색(DFS, BFS)을 포스팅하려고
그래프와 트리 내용을 적고 있었는데 생각보다 길어져, 그래프와 트리 포스팅을 따로 해봤습니다.
전날 과음으로 숙취에 시달리면서, 다시는 오전수업을 안듣겠다 다짐하며
알고리즘/자료구조 시간을 들을 땐 몰랐습니다.
그래프와 트리. 컴퓨터 공학에서 정말 중요한 녀석들이였습니다.
아니 자료구조와 알고리즘 자체가 컴퓨터 공학에서 매우 중요했지요.
사실 CS 지식을 배우며 이론... 노잼.... 하며 투덜거렸는데,
지금 생각해보면 정말 무엇 하나 뺄 것 없이 하나 하나 매우 중요한 것들어였던 것 같습니다.
'CS 지식 > 자료구조' 카테고리의 다른 글
| [자료구조] 스택, 큐, 데크 - 자료구조 삼대장 (0) | 2023.07.15 |
|---|---|
| [자료구조] 그래프의 표현 방법: 인접 행렬과 인접 리스트 (0) | 2023.07.13 |
| [자료구조] 분리 집합(Disjoint set)과 유니온 - 파인드(Union-Find) (0) | 2022.11.04 |

