

이분 매칭을 간단히 이야기하면 연애 매칭 프로그램입니다.
남과 여 두 그룹이 있고,
남 -> 여 혹은 여 -> 남으로 맘에 드는 이성을 골랐을 때,
커플이 가장 많이 매칭되는 경우를 찾는 것이지요.
좋은 예시가 없을까 하며 돌아다니다가,
MIT 오픈 코스 유튜브에서 남과 여를 매칭하는 걸 예로 들길래
이거다! 하고 참고해서 포스팅해봤습니다.
https://www.youtube.com/watch?v=HZLKDC9OSaQ&ab_channel=MITOpenCourseWare
이분 그래프

이분 그래프는 k분 그래프의 일종으로 k=2인 경우의 그래프입니다.
k분 그래프는 아래와 같이 나타낼 수 있는데요.
집합 V(i), V(j) 가 있다고 했을 때

쉽게 말해서 간선의 양 끝은 서로 다른 그룹이여야 한다는 의미입니다.
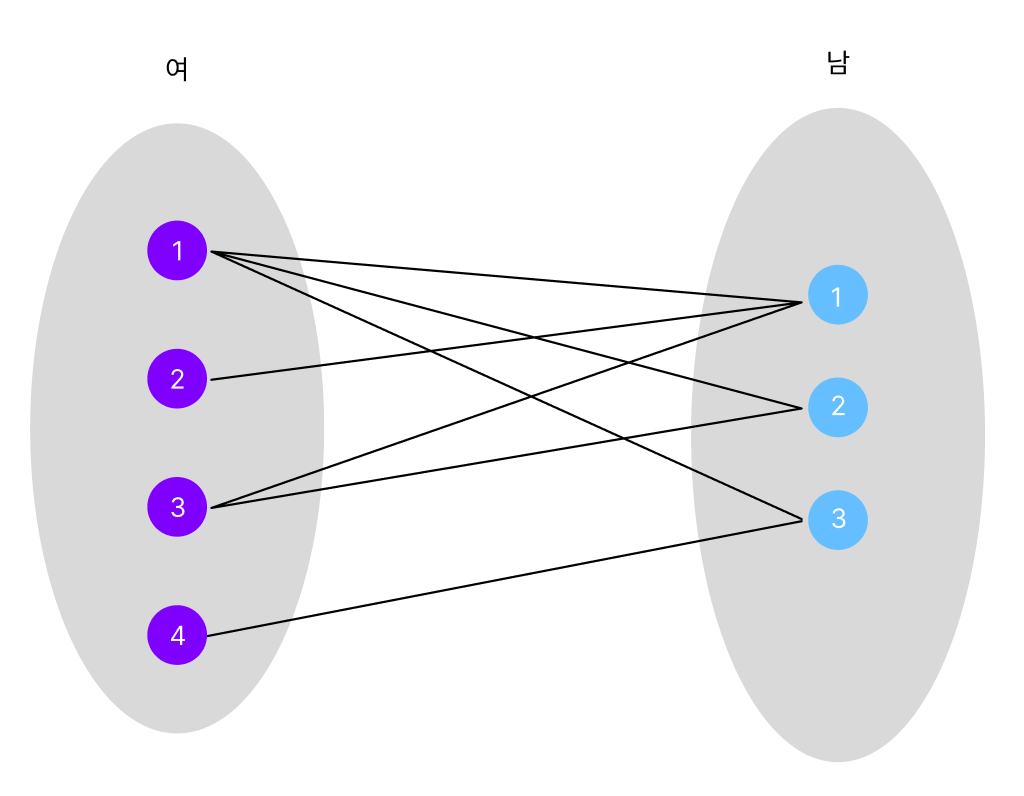
연애 프로그램을 예로 들면
남-녀 두 집합이 있을 때,
남성 참가자는 여성 참가자를 선택해야 하고,
여성 참가자는 남성 참가자를 선택해야 한다는 의미입니다.
단, 그래프의 방향은 양방향 혹은 한 그룹에서 다른 그룹으로 가는 방향만 존재해야 합니다.

예를 들어 위와 같이 남 -> 여, 여 -> 남 방향 간선이 둘 다 존재할 경우에는 이분 매칭을 사용할 수 없습니다.
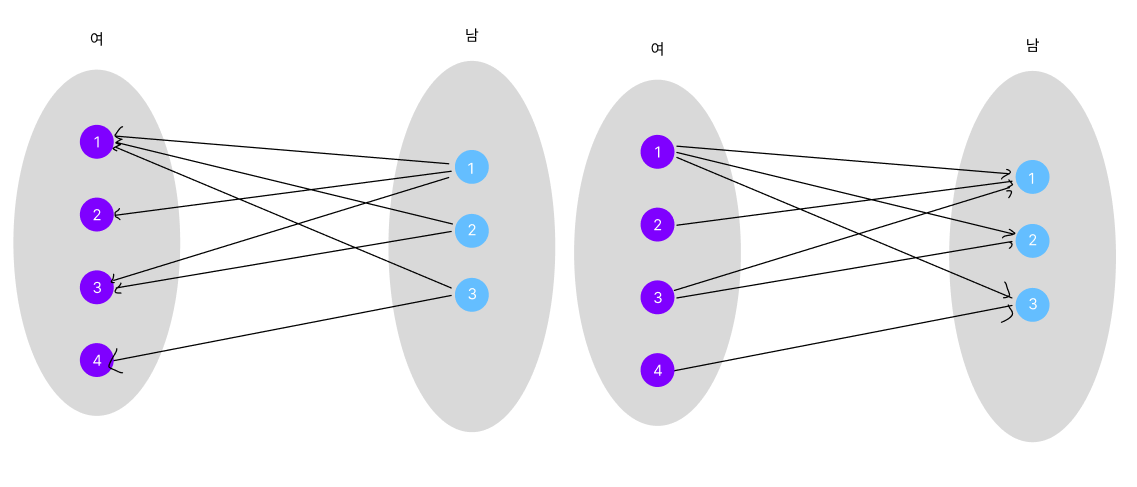
남성 참가자만 여성 참가자를 선택하거나,
여성 참가자만 남성 참가자를 선택하는 경우.
즉, 집합 X, Y에 대해 간선의 방향이 X -> Y 만 존재하는 경우 혹은 Y -> X만 존재하는 경우에 한해
이분 매칭 알고리즘을 사용할 수 있습니다.
이분 매칭 (Bipartite Matching)
이분 매칭은 네트워크 플로우의 일종으로 볼 수 있습니다.
다만, DFS를 사용하여 이분 그래프에서 좀 더 특화된 코드를 작성할 수 있습니다.

위와 같은 호감 표시 관계도가 있을 때,
여 1부터 시작해 매칭해봅시다.

여1과 남1을 매칭했습니다.
그러나 여2가 남1에게만 호감을 표시하고 있습니다.

때문에 여1을 남2와 매칭하고,
여2를 남1과 매칭합니다.
앗! 그런데 여3이 이미 매칭된 남1과 남2에게만 호감을 보냈습니다!

여1을 남3에게 매칭하고,
여3을 남2에게 매칭했습니다.
더 이상 매칭이 불가능하기에 이분 매칭 알고리즘을 종료합니다.
DFS를 사용한 구현 : 실제 문제 풀어보기
위 이분 매칭 알고리즘은 DFS를 사용해 구현할 수 있습니다.
그럼 이분 매칭을 연습하기 좋은 백준 1298 - '노트북의 주인을 찾아서'를 봅시다.
https://www.acmicpc.net/problem/1298
1298번: 노트북의 주인을 찾아서
어느 날 모든 학생들은 한 명이 한개의 노트북을 가지고 공부하던 도중, 자리를 바꾸다가 그만 노트북이 뒤섞이고 말았다. 대다수의 학생들은 자신의 노트북을 잘 알고 있어서 자신의 노트북을
www.acmicpc.net
학생들이 자리를 바꾸다가 그만 노트북이 뒤섞이고 말았습니다!
학생들은 바로 어제 노트북을 샀기에, 대다수가 자기 노트북을 구분하지 못하였고,
자기 물건인 것 같은 노트북들을 말해보라 했습니다.
"이거 아니면 이거 아니면 이거일것 같아요" 라는 이야기를 듣고,
학생들과 학생들이 생각하는 자신의 노트북 후보를 그래프로 아래와 같이 나타내봤습니다.
이 때, 만족하는 학생의 수가 최대가 되도록 매칭을 시켜봅시다!

전체 소스코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
public class Main {
static boolean[] visited; // 노드 방문 여부
static int[] matchedStudent; // 노트북의 주인 학생 번호
static ArrayList<Integer>[] graph; // 학생 : 자신의 것으로 추정되는 노트북 연결정보
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] nm = br.readLine().split(" ");
int n = Integer.parseInt(nm[0]);
int m = Integer.parseInt(nm[1]);
graph = new ArrayList[n + 1];
matchedStudent = new int[n + 1];
for (int i = 1; i <= n; i++) {
graph[i] = new ArrayList<>();
}
for (int i = 1; i <= n; i++) {
matchedStudent[i] = -1;
}
for (int i = 1; i <= m; i++) {
String[] input = br.readLine().split(" ");
int studentNum = Integer.parseInt(input[0]);
int notebookNum = Integer.parseInt(input[1]);
graph[studentNum].add(notebookNum);
}
int result = 0;
for (int i = 1; i <= n; i++) {
visited = new boolean[n + 1];
if (dfs(i)) {
result++;
}
}
System.out.println(result);
}
public static boolean dfs(int node) {
if (visited[node]) {
return false;
}
visited[node] = true;
for (int i = 0; i < graph[node].size(); i++) {
int next = graph[node].get(i);
if (matchedStudent[next] == -1 || dfs(matchedStudent[next])) {
matchedStudent[next] = node;
return true;
}
}
return false;
}
}
int[] matchedStudent는 각 노트북에게 매칭된 학생을 담을 배열입니다.
초기값을 -1로 지정하여, 매칭된 학생이 아직 없음을 표기해줍시다.
graph는 각 학생 : 자신의 것으로 생각되는 노트북 정보를 그래프로 담고 있습니다
visited는 각 학생을 방문했는지 여부입니다. 중복 방문을 체크하기 위함입니다.
DFS
public static boolean dfs(int node) {
if (visited[node]) {
return false;
}
visited[node] = true;
for (int i = 0; i < graph[node].size(); i++) {
int next = graph[node].get(i); // 노트북 번호
if (matchedStudent[next] == -1 || dfs(matchedStudent[next])) { // 노트북이 아무도 없거나, 노트북을 가진 학생이 다른 노트북을 가질 수 있는 경우
matchedStudent[next] = node;
return true;
}
}
return false;
}
이미 처리를 완료한 (visited[node] == true) 학생일 경우 조기 return을 해주고,
처리를 완료하지 않은 학생의 경우에만 로직을 수행합니다.
학생들은 자신의 것으로 추정되는 노트북들이
아직 주인이 없거나(-1)
노트북을 가진 학생이 다른 노트북을 가질 수 있는 경우 (dfs(matchStudent[next] == true)일 경우,
해당 노트북을 자신의 것으로 체크하고 true를 반환합니다.
학생 A가 노트북 1을 자신의 것으로 생각하고 있는데,
노트북 1의 주인이 이미 학생 B로 마킹이 되어있다면,
학생 A가 학생 B에게 가서
혹시나 학생 B가 노트북 1 말고도 다른 노트북(노트북 2, 노트북 3 등)을 자신의 것으로 생각하고 있다면
학생 B는 노트북 2를 자신의 것으로 마킹하고,
노트북 1을 학생 A에게 '양보' 하는 것으로 생각할 수 있습니다.
위 과정을 반복하여 최종적으로 최대 다수가 만족할 수 있는 경우를 찾아내는 것이지요.
int result = 0;
for (int i = 1; i <= n; i++) {
visited = new boolean[n + 1];
if (dfs(i)) {
result++;
System.out.println(i + " 번째 수행");
for (int j = 1; j <= n; j++) {
System.out.println(j + "번 노트북 주인 학생 : " + matchedStudent[j] + "번 학생");
}
System.out.println();
}
}
System.out.println(result);
=====================================================
1 번째 수행
1번 노트북 주인 학생 : -1번 학생
2번 노트북 주인 학생 : 1번 학생
3번 노트북 주인 학생 : -1번 학생
4번 노트북 주인 학생 : -1번 학생
5번 노트북 주인 학생 : -1번 학생
2 번째 수행
1번 노트북 주인 학생 : -1번 학생
2번 노트북 주인 학생 : 2번 학생
3번 노트북 주인 학생 : 1번 학생
4번 노트북 주인 학생 : -1번 학생
5번 노트북 주인 학생 : -1번 학생
3 번째 수행
1번 노트북 주인 학생 : 3번 학생
2번 노트북 주인 학생 : 2번 학생
3번 노트북 주인 학생 : 1번 학생
4번 노트북 주인 학생 : -1번 학생
5번 노트북 주인 학생 : -1번 학생
5 번째 수행
1번 노트북 주인 학생 : 3번 학생
2번 노트북 주인 학생 : 2번 학생
3번 노트북 주인 학생 : 1번 학생
4번 노트북 주인 학생 : 5번 학생
5번 노트북 주인 학생 : -1번 학생
각 학생의 매칭(DFS) 완료 시점마다 로그를 찍어보면,
각 단계마다 어떻게 매칭이 이뤄지는지 보다 수월하게 알 수 있습니다.
후기
이분 매칭 알고리즘이 어떻게 동작하는지 이해 자체는 빨리 되었는데,
코드가 어떻게 동작하는지 이해하는데 꽤나 걸렸던 것 같습니다.
https://www.youtube.com/watch?v=HZLKDC9OSaQ&ab_channel=MITOpenCourseWare
'CS 지식 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 에라토스테네스의 체 (Sieve of Eratosthenes) (0) | 2024.01.30 |
|---|---|
| 알고리즘 성능 평가 [2] : 공간 복잡도(Space Complexity) (2) | 2023.08.21 |
| 알고리즘 성능 평가 [1] : 시간 복잡도(Time Complexity) (0) | 2023.08.20 |
| [알고리즘] 그래프 탐색 - 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS) (0) | 2023.07.18 |
| [알고리즘] 최소 스패닝 트리 (MST, Minimum Spanning Tree) (0) | 2023.04.24 |
