https://www.acmicpc.net/problem/1939
1939번: 중량제한
첫째 줄에 N, M(1 ≤ M ≤ 100,000)이 주어진다. 다음 M개의 줄에는 다리에 대한 정보를 나타내는 세 정수 A, B(1 ≤ A, B ≤ N), C(1 ≤ C ≤ 1,000,000,000)가 주어진다. 이는 A번 섬과 B번 섬 사이에 중량제한이
www.acmicpc.net
난이도 : 골드 3
태그 : 자료 구조, 그래프 이론, 그래프 탐색, 이분 탐색, 너비 우선 탐색, 분리 집합
설명
N개의 섬들은 M개의 다리를 통해 서로 연결 되어있습니다.
각 다리에는 중량 제한이 있고, 중량 제한을 초과할 경우 다리가 무너집니다.
한 번에 이동할 수 있는 중량의 최댓값을 구하는 문제입니다.
가장 빨리 떠오른 생각은 브루트포스적으로 접근하여
다리의 최소 중량 ~ 최대 중량의 값에 대해 모두 BFS를 돌려볼까? 싶었지만,
C의 범위 (1 ≤ C ≤ 1,000,000,000)를 보고 빠르게 다른 해결방안을 고민했습니다.
두 번째 떠오른 생각은 BFS + 이분 탐색 입니다.
https://uknowblog.tistory.com/321
[백준 2805번] [Kotlin] 나무 자르기
https://www.acmicpc.net/problem/2805 2805번: 나무 자르기 첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 1,000,000, 1 ≤ M ≤ 2,000,000,000) 둘째 줄에는 나무의
uknowblog.tistory.com
위의 나무 자르기 문제와 마찬가지로,
이분 탐색으로 다리 중량의 최솟값 ~ 최댓값을 대상으로 이분 탐색을 하며,
탐색값에 대해 BFS를 돌며 가능하다면 왼쪽쪽 반절을 대상으로,
불가능하다면 오른쪽 반절을 대상으로 해를 찾는 방법이 있습니다.
예전에는 위 방법(BFS+이분탐색)으로 해결하였으나,
오랜만에 이 문제를 다시 보니, 백준 13905 '세부' 문제가 떠올랐어요.
https://www.acmicpc.net/problem/13905
13905번: 세부
첫 번째 줄에는 섬에 존재하는 집의 수 N(2≤N≤100,000)와 다리의 수 M(1≤M≤300,000)이 주어진다. 두 번째 줄에는 숭이의 출발 위치(s)와 혜빈이의 위치(e)가 주어진다. (1≤s, e≤N, s≠e). 다음 M개의 줄
www.acmicpc.net
흠.. 최소 스패닝 트리(분리 집합, 유니온 - 파인드)로 풀 수도 있을 것 같네요.

위와 같은 예제가 주어졌다고 가정해봅시다.
각 노드는 섬, 간선은 다리이며, s는 출발 노드, e는 도착 노드입니다.
간선 옆에 적힌 숫자는 각 다리의 가중치(중량 제한) 입니다.
각 간선의 가중치(중량 제한)이 적은 순서대로 선택해봅시다.
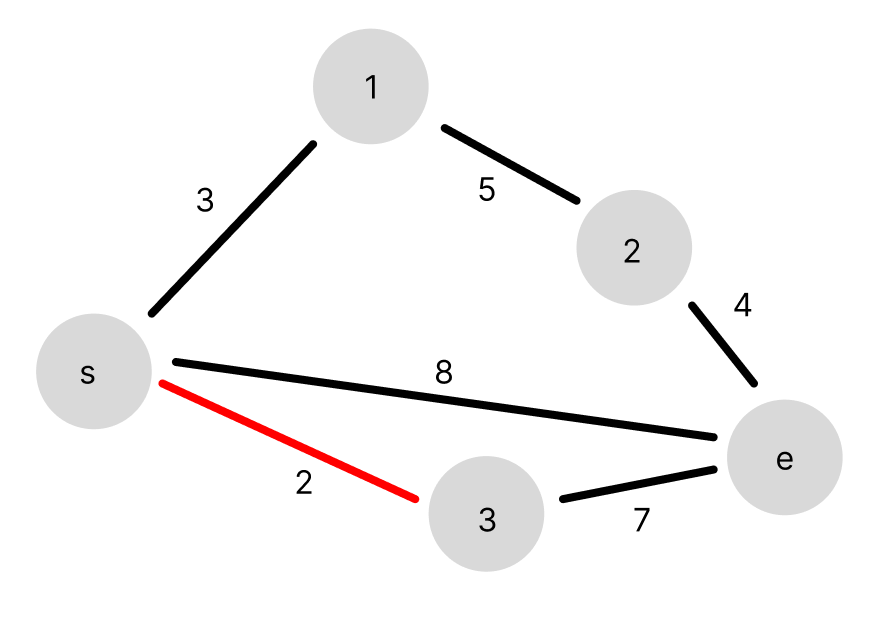
s노드와 3번 노드가 연결되었습니다.
하지만 s노드에서 e노드로 가는 경로는 아직 없습니다.
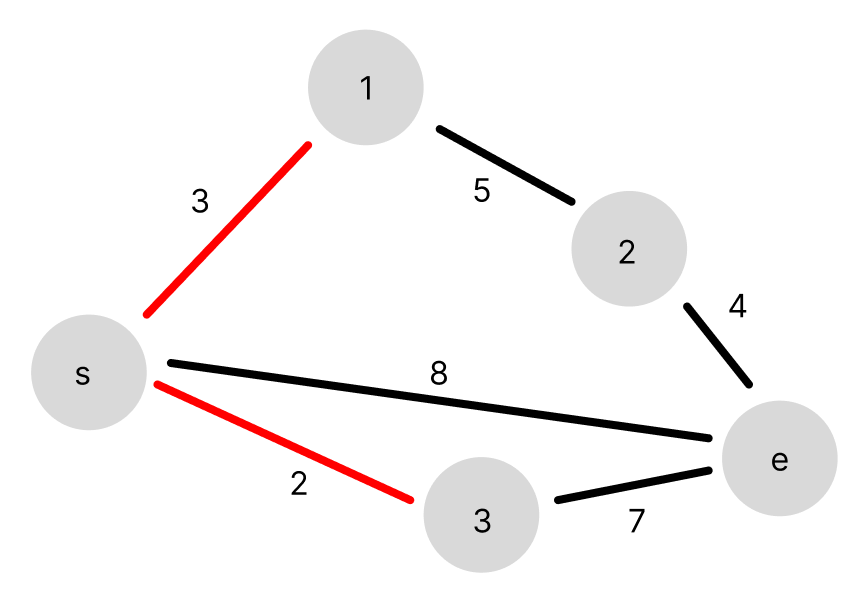
가중치가 3인 간선을 이어줬습니다.
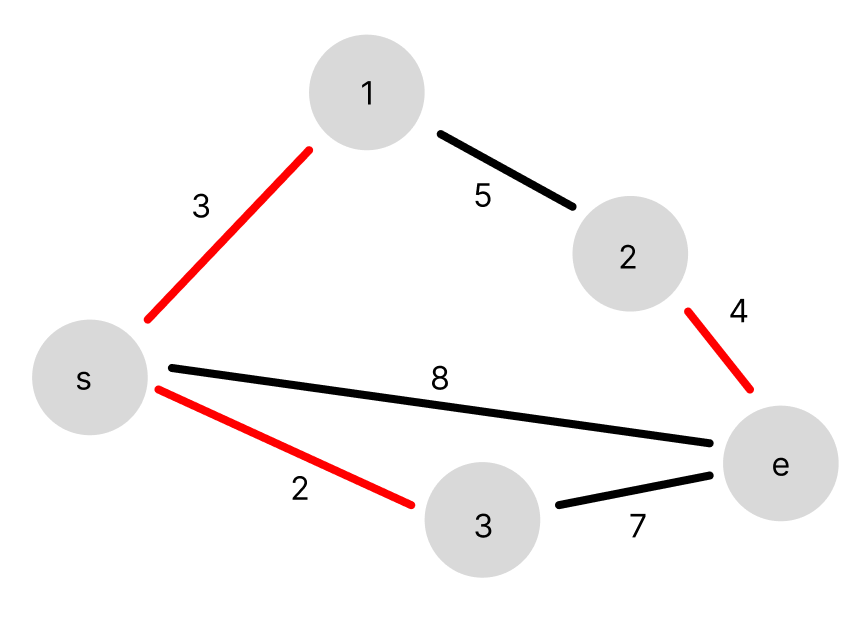
가중치가 4인 간선을 이어줬습니다.
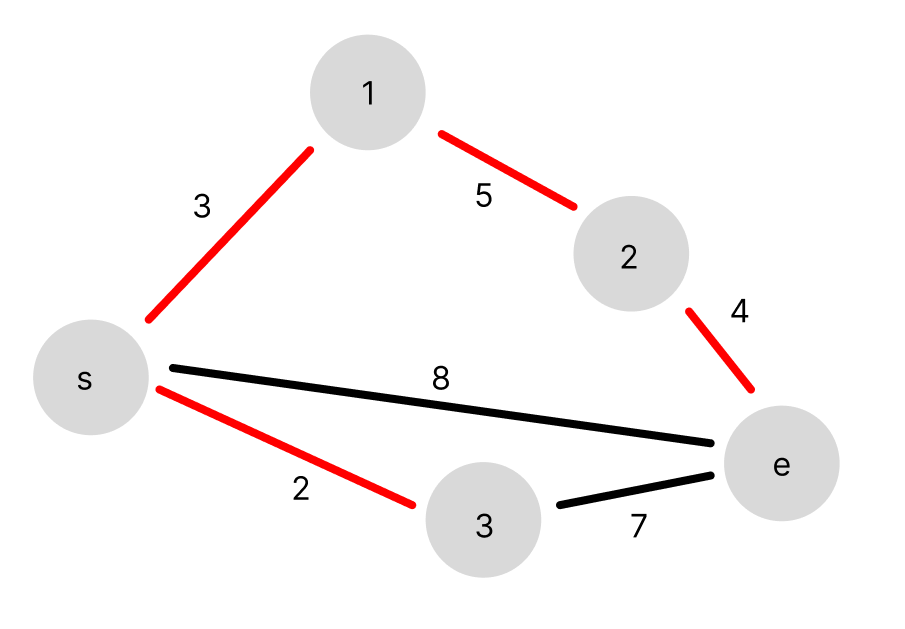
가중치가 5인 간선을 이어줬습니다.
s 노드에서 e 노드로 가는 경로가 생겼습니다!
따라서 해당 그래프에서 s 노드에서 e 노드로 가는 최소 가중치 (중량 제한)이 5임을 알 수 있습니다.
위 과정을 보면 아시겠지만, 분리집합+유니온파인드를 사용해
최소 스패닝 트리를 만드는 과정과 아주 유사합니다.
소스코드
이분 탐색 + BFS를 사용한 방법
import java.util.LinkedList
import java.util.Queue
data class Edge(val to: Int, val weight: Int)
var n = 0
lateinit var connect: Array<ArrayList<Edge>>
var start = 0
var end = 0
fun main() = with(System.`in`.bufferedReader()) {
val nm = readLine().split(" ").map(String::toInt)
n = nm[0]
val m = nm[1]
connect = Array(n + 1) { ArrayList() }
var (left, right) = arrayOf(Int.MAX_VALUE, 0)
repeat(m) {
val (from, to, weight) = readLine().split(" ").map(String::toInt)
connect[from].add(Edge(to, weight))
connect[to].add(Edge(from, weight))
left = minOf(left, weight)
right = maxOf(right, weight)
}
val se = readLine().split(" ").map(String::toInt)
start = se[0]
end = se[1]
var answer = 0
while (left <= right) {
val mid = (left + right) / 2
if (bfs(mid)) {
answer = mid
left = mid + 1
} else {
right = mid - 1
}
}
print(answer)
}
fun bfs(maxWeight: Int): Boolean {
val queue = LinkedList<Int>() as Queue<Int>
val visited = BooleanArray(n + 1) { false }
queue.offer(start)
visited[start] = true
while (queue.isNotEmpty()) {
val cur = queue.poll()
connect[cur].forEach { next ->
if (visited[next.to] || next.weight < maxWeight) return@forEach
if (next.to == end) return true
queue.offer(next.to)
visited[next.to] = true
}
}
return false
}
이분 탐색 + BFS를 사용한 풀이입니다.
각 간선의 최소치와 최대치를 left, right 값으로 세팅한 뒤,
이분 탐색을 진행해가며 탐색값에 대해 BFS를 돌립니다.
최솟값이 3, 최댓값이 17일 경우, 둘의 평균인 10을 대상으로
BFS를 돌며 중량 제한 10 안에 S에서 E를 도달할 수 있다면
좌측 반절을, 도달할 수 없다면 우측 반절을 대상으로 다음 탐색을 진행해가며 해를 찾아갑니다.
분리 집합을 사용한 방법
import java.util.PriorityQueue
data class Edge(val from: Int, val to: Int, val weight: Int)
lateinit var parent: IntArray
fun main() = with(System.`in`.bufferedReader()) {
val (n, m) = readLine().split(" ").map { it.toInt() }
parent = IntArray(n + 1) { it }
val pq = PriorityQueue<Edge>(compareBy { -it.weight })
repeat(m) {
val (from, to, weight) = readLine().split(" ").map { it.toInt() }
pq.offer(Edge(from, to, weight))
}
val (start, end) = readLine().split(" ").map { it.toInt() }
while (pq.isNotEmpty()) {
val (from, to, weight) = pq.poll()
if (union(from, to)) {
if (find(start) == find(end)) {
println(weight)
return
}
}
}
}
fun find(x: Int): Int {
if (parent[x] == x) return x
parent[x] = find(parent[x])
return parent[x]
}
fun union(x: Int, y: Int): Boolean {
val (px, py) = find(x) to find(y)
if (px == py) return false
parent[py] = px
return true
}
간선의 가중치(중량 제한)이 작은 순으로 sort 한 뒤,
분리집합을 사용해,
간선을 하나씩 선택해가며 간선의 양 끝에 연결된 노드의 부모를 동일하게 만들어줍니다.
각 간선이 이어질 때 마다 S 노드와 E 노드가 같은 부모인지 확인합니다.
S 노드와 E 노드의 부모가 같아지는 순간,
두 노드가 이어진 것이므로 해당 가중치 값을 출력하고 종료합니다.
후기
여러 방법으로 접근할 수 있어 굉장히 좋은 문제라 생각합니다.
해당 포스팅에서 언급한 이분탐색, BFS, 최소스패닝트리, 분리집합 말고도
다익스트라를 통해서도 풀 수도 있다고 하네요.
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [백준 1385번] [Kotlin] 벌집 (2) | 2024.01.30 |
|---|---|
| [백준 1017번] [Kotlin] 소수 쌍 (0) | 2024.01.28 |
| [백준 10216번] [Kotlin] Count Circle Groups (1) | 2024.01.05 |
| [백준 3184번] [Kotlin] 양 (1) | 2023.12.30 |
| [백준 21610번] [Kotlin] 마법사 상어와 비바라기 (1) | 2023.12.27 |
