https://www.acmicpc.net/problem/2623
2623번: 음악프로그램
첫째 줄에는 가수의 수 N과 보조 PD의 수 M이 주어진다. 가수는 번호 1, 2,…,N 으로 표시한다. 둘째 줄부터 각 보조 PD가 정한 순서들이 한 줄에 하나씩 나온다. 각 줄의 맨 앞에는 보조 PD가 담당한
www.acmicpc.net
난이도 : 골드3
태그 : 그래프 이론, 위상정렬
1. 설명
누가 누구보다 더 앞선 우선순위를 갖고 있다는 사실만으로 정렬을 하는 위상정렬 문제입니다.
예를 들어 A, B, C, D, E. 5명의 사람을 키 순서대로 정렬하려 할때,
170cm, 180cm, 190cm, 160cm, 150cm 등으로 각 사람의 키가 주어지면
손쉽게 정렬 할 수 있겠지만,
A는 B보다 작다.
D, E는 C보다 작다.
A는 D보다 크다.
B는 D보다 크다. 와 같이
누가 누구보다 크다(=누가 누구보다 우선순위가 높다)는 사실만을 갖고 정렬할때 쓰이는 알고리즘 입니다.
예제를 보고 한 번 설명해 보겠습니다.
- 1 4 3
- 6 2 5 4
- 2 3
1번 PD는 1 -> 4 -> 3,
2번 PD는 6 -> 2 -> 5 -> 4,
3번 PD는 2 -> 3
순서대로 각 가수의 순서를 정했습니다.
2보다 1, 6번 가수가 먼저 나와야 하며,
3번 가수보다 2, 4번 가수가 먼저 나와야 하고,
4번 가수보다 1, 5번이,
5번 가수보다 2번이 앞에 나와야 합니다.
이와 같이, A가 B보다 우선순위가 높다. 라는 정보만 가지고 정렬을 할 때에는 위상정렬 알고리즘을 사용합니다.
2. 위상 정렬
위상정렬 알고리즘은 다음과 같습니다.
1. 진입차수가 0인 노드를 큐에 삽입
2. 큐에서 하나씩 꺼내 연결된 노드의 간선 제거
3. 새롭게 진입차수가 0인 노드 큐에 추가
이 과정을 큐가 빌 때 까지 반복합니다.

예제의 관계를 숫자의 중복 없이 그래프로 표현하면 위와 같습니다.
또, 각 가수의 진입차수(자기를 향한 화살표가 얼마나 있는지)를 나타내면 아래 표와 같습니다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1 | 2 | 2 | 1 | 0 |
진입차수가 0인 노드부터 큐에 담고,
큐에서 하나씩 노드를 꺼내 연결된 간선을 제거합니다.
여기선 1과 6중 어느것을 먼저 큐에 넣어도 무방하나, 예제처럼 6번 가수를 먼저 큐에 넣고, 1번을 넣겠습니다.
현재 큐 : 6 ,1
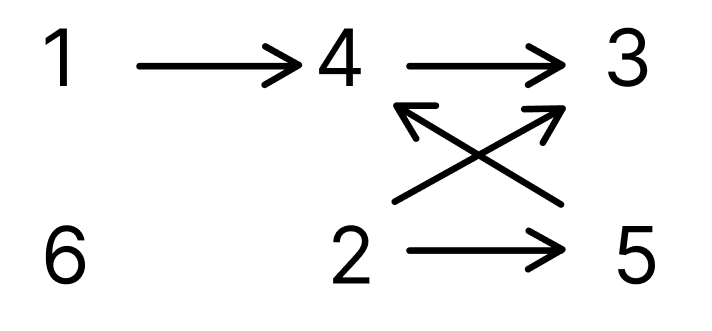
간선을 제거한 모습입니다.
각 노드의 진입차수는 다음과 같습니다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 2 | 2 | 1 | 0 |
진입차수가 0이 된 2번 노드를 큐에 넣습니다.
현재 큐 : 1, 2 (poll - 6)
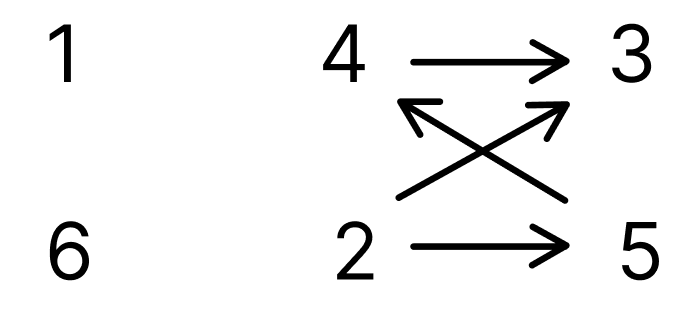
1번 노드를 큐에서 꺼내 간선을 제거한 모습입니다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 2 | 1 | 1 | 0 |
진입차수가 0이 된 2번 노드를 큐에 넣습니다.
새롭게 진입차수가 0이 된 노드는 없으니 다음으로 넘어갑니다.
현재 큐 : 2 (poll - 6, 1)
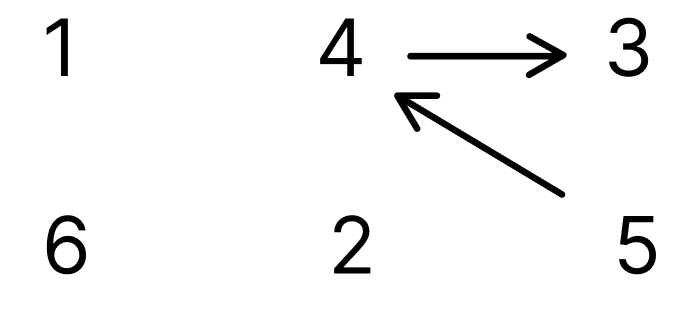
2번 노드를 큐에서 꺼내 간선을 제거한 모습입니다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 1 | 0 | 0 |
새롭게 진입차수가 0이 된 5번 노드를 큐에 넣습니다.
현재 큐 : 5 ( poll - 6, 1, 2)
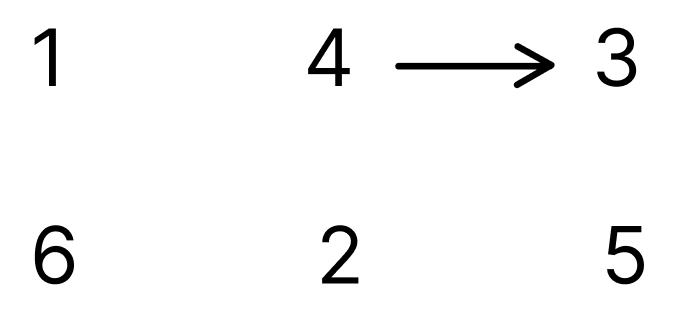
5번 노드를 큐에 꺼내 간선을 제거합니다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 1 | 0 | 0 | 0 |
4번을 큐에 넣습니다.
현재 큐 : 4 ( poll - 6, 1, 2, 5 )

| 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0 | 0 | 0 | 0 | 0 |
4번을 큐에서 꺼내 간선을 제거한 모습입니다.
모든 정점의 진입차수가 0이 되었습니다.
큐에서 꺼낸 순서는 다음과 같습니다.
6, 1, 2, 5, 4, 3
즉, 큐에서 꺼낸 순서가 곧 정렬된 순서 입니다.
3. 소스코드
3.1. 인풋값 세팅
<code />
val br = BufferedReader(InputStreamReader(System.`in`))
val nm = br.readLine().split(" ")
val n = nm[0].toInt() // 가수의 수
val m = nm[1].toInt() // PD의 수
val result = ArrayList<Int>()
val inDegree = Array(n + 1) { 0 }
val connectedNode = Array(n + 1) { ArrayList<Int>() }
for (i in 1..m) {
val line = br.readLine().split(" ").map { it.toInt() }
for (j in 2..line[0]) {
inDegree[line[j]]++
connectedNode[line[j - 1]].add(line[j])
}
}
각 가수의 진입차수와 연결된 가수를 초기화합니다.
inDegree는 진입차수,
connectedNode는 연결된 다음 가수를 의미합니다.
3.2. 위상정렬
<code />
val q: Queue<Int> = LinkedList()
repeat(n) { if (inDegree[it + 1] == 0) q.offer(it + 1) }
for (i in 1..n) {
if (q.isEmpty()) {
println("0") // 큐가 빔. 사이클 발생...
return
}
val target = q.poll()
result.add(target)
for (j in 0 until connectedNode[target].size) {
val y = connectedNode[target][j]
if (--inDegree[y] == 0) {
q.offer(y)
}
}
}
진입차수가 0인 노드를 큐에 삽입하고,
모든 노드를 방문하면서 각 노드에 연결된 간선을 제거합니다.
간선을 제거한 이후, 진입차수가 0인 노드는 큐에 삽입합니다.
만약, 모든 노드를 방문하기 전에 큐가 빈다면 사이클이 발생한 것이므로
0을 출력하고 프로그램을 종료합니다.
큐에서 꺼내는 순서가 곧 정렬된 순서이므로, 큐에서 꺼낼때마다 result 배열에 담아줍니다.
3.3. 전체 소스코드
<javascript />
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.LinkedList
import java.util.Queue
import kotlin.math.sign
fun main() {
val br = BufferedReader(InputStreamReader(System.`in`))
val nm = br.readLine().split(" ")
val n = nm[0].toInt() // 가수의 수
val m = nm[1].toInt() // PD의 수
val result = ArrayList<Int>()
val inDegree = Array(n + 1) { 0 }
val connectedNode = Array(n + 1) { ArrayList<Int>() }
for (i in 1..m) {
val line = br.readLine().split(" ").map { it.toInt() }
for (j in 2..line[0]) {
inDegree[line[j]]++
connectedNode[line[j - 1]].add(line[j])
}
}
val q: Queue<Int> = LinkedList()
repeat(n) { if (inDegree[it + 1] == 0) q.offer(it + 1) }
for (i in 1..n) {
if (q.isEmpty()) {
println("0") // 큐가 빔. 사이클 발생...
return
}
val target = q.poll()
result.add(target)
for (j in 0 until connectedNode[target].size) {
val y = connectedNode[target][j]
if (--inDegree[y] == 0) {
q.offer(y)
}
}
}
result.forEach {
println(it)
}
}
4. 후기
위상정렬을 평소 잘 접해보지 않아서,
위상정렬 알고리즘이 뭔지 공부해가면서 풀었던 문제입니다.
Solved.ac의 클래스 3까진 그래도 나름 할만했는데,
4~5클래스 문제들은 특정 알고리즘을 알지 못하면 풀지 못하는 문제가 꽤 있는 것 같습니다.
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [백준 1600번] [Kotlin] 말이 되고픈 원숭이 (1) | 2022.10.03 |
|---|---|
| [백준 1043번][Kotlin] 거짓말 (분리집합, Union-Find 사용) (0) | 2022.09.28 |
| [백준 2239번][Kotlin] 스도쿠 (0) | 2022.09.17 |
| [백준 1987번][Kotlin] 알파벳 (0) | 2022.08.21 |
| [백준 11404번][Kotlin] 플로이드 (0) | 2022.08.18 |

