https://www.acmicpc.net/problem/13905
13905번: 세부
첫 번째 줄에는 섬에 존재하는 집의 수 N(2≤N≤100,000)와 다리의 수 M(1≤M≤300,000)이 주어진다. 두 번째 줄에는 숭이의 출발 위치(s)와 혜빈이의 위치(e)가 주어진다. (1≤s, e≤N, s≠e). 다음 M개의 줄
www.acmicpc.net
난이도 : 골드 4
태그 : 자료 구조, 그래프 이론, 그래프 탐색, 분리 집합, 최소 스패닝 트리
설명

한 섬에서 다른 섬으로 가지만,
다리(간선)가 버틸 수 있는 문제가 한정되어 있어,
가중치의 최솟값이 최대가 되야 합니다.
가중치의 최솟값이 최대가 되야 한다... 이게 무슨 말인가 싶긴 하지만,
위 그래프를 예시로 들 때, 1번 집에서 5번 집으로 가야 합니다.
하지만 1 -> 2 -> 3 -> 5로 갈 경우, 2 -> 3은 가중치(버틸 수 있는 무게)가 5지만,
1 -> 2, 3 -> 5의 가중치(버틸 수 있는 무게)가 2이기 때문에,
최종적으로 1 -> 2 -> 3 -> 5 루트는 총 2의 금빼빼로를 들고갈 수 있습니다.
반면 1 -> 7 -> 6 -> 3의 경우,
1 -> 7은 4, 7 -> 6은 4지만, 6 -> 5의 가중치는 3으로,
가중치의 최솟값이 3입니다.
따라서 1 -> 2 -> 3 -> 5의 가중치의 최솟값은 2,
1 -> 7 -> 6 -> 3의 가중치의 최솟값은 3으로,
가중치의 최솟값이 가장 큰 1 -> 7 -> 6 -> 3이 되는 것 입니다.
즉, 해당 문제는 한 정점으로부터 다른 정점으로 가되,
거치는 노드의 수나 가중치의 합에 관계 없이, 간선의 가중치의 최솟값에 달려있습니다.
즉, 그리디하게 접근하여 가중치가 큰 간선부터 양쪽 노드를 이어주면서,
시작 노드로부터 도착 노드로가는 경로가 생기는 순간,
마지막으로 이어줬던 간선의 가중치가 정답이 됩니다!

문제의 예시로 나온 그래프를 사용해 시뮬레이션 해보겠습니다.
출발노드는 1, 도착노드는 5입니다.

가중치(버틸 수 있는 무게) 중 가장 큰 값은 5입니다.
가중치가 5인 간선부터 서로 이어줍니다.
아직 1번 노드에서 5번 노드로 가는 경로가 없습니다.
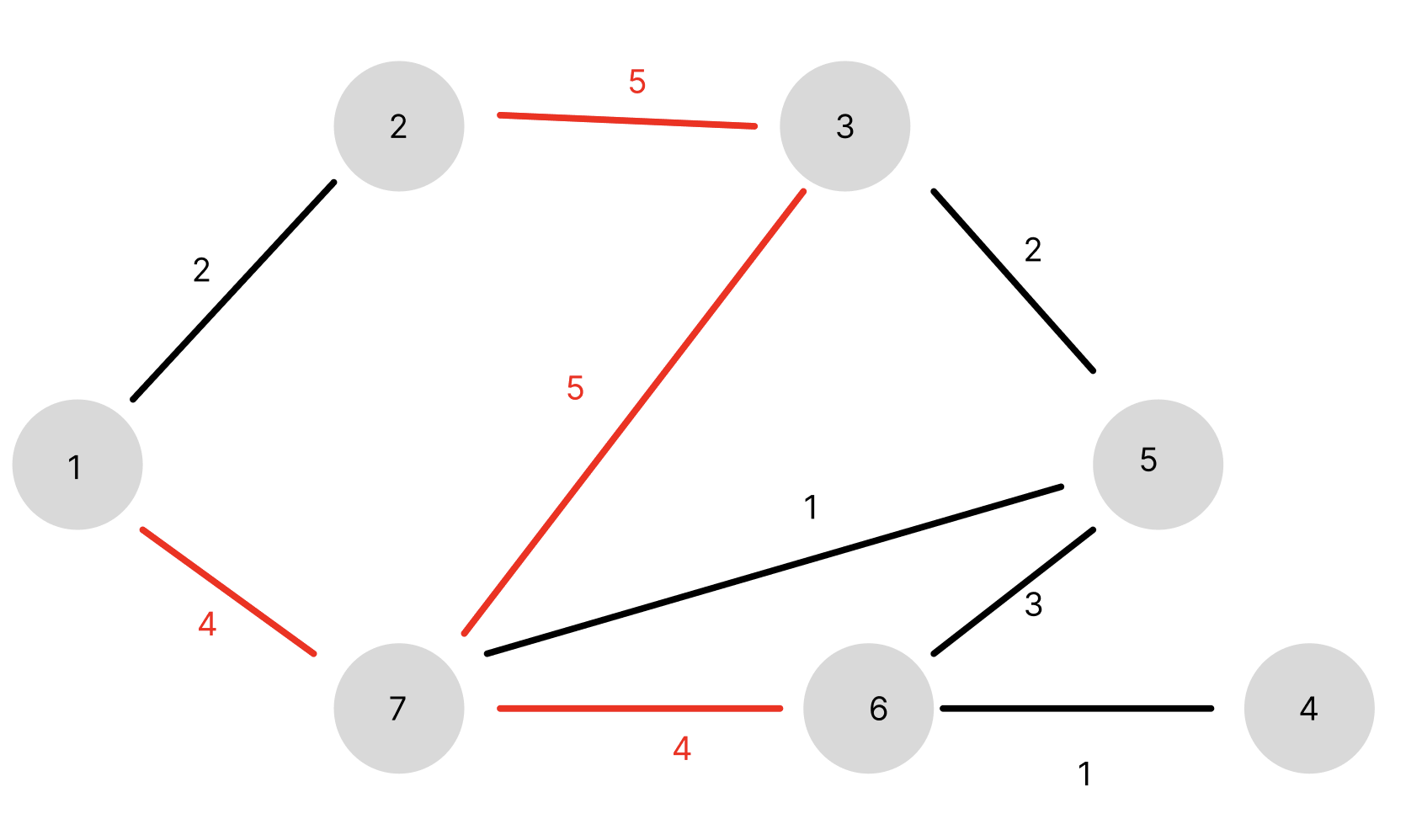
5 다음으로 큰 가중치는 4입니다.
4만큼의 가중치를 가지는 간선도 이어줬지만, 아직 1번 노드에서 5번 노드로 가는 경로가 없습니다.

5, 4 다음으로 큰 가중치인 3을 이어줬습니다.
1 -> 7 -> 6 -> 5로, 1번 노드에서 5번 노드로 가는 경로가 생겼습니다!
가중치가 3인 간선을 이어줌으로써, 1->5 경로가 생겼으니, 이 예제의 답은 3입니다.
그런데, 위 과정... 좀 익숙합니다.
그리디하게 접근해 가장 큰(작은) 간선부터 연결...?
네, 크루스칼 알고리즘 기반의 최소 스패닝 트리와 비슷한 원리로 풀 수 있습니다.
다만 가중치가 작은 것 부터가 아닌 큰 것부터 선택하되,
시작 노드와 도착 노드가 이어지면 더 이상 프로그램을 수행할 필요가 없어질 뿐 입니다.
시작 노드와 도착 노드가 서로 연결되었는지 역시
분리 집합과 유니온 - 파인드 알고리즘으로 두 노드가 연결되었는지 알 수 있습니다.
소스코드
data class Edge(val from: Int, val to: Int, val cost: Int)
lateinit var parent: IntArray
fun main() = with(System.`in`.bufferedReader()) {
val (n, m) = readLine().split(" ").map { it.toInt() }
val (s, e) = readLine().split(" ").map { it.toInt() }
parent = IntArray(n + 1) { it }
val edges = ArrayList<Edge>()
for (i in 0 until m) {
val (from, to, cost) = readLine().trim().split(" ").map { it.toInt() }
edges.add(Edge(from, to, cost))
}
edges.sortByDescending { it.cost }
for ((from, to, cost) in edges) {
if (union(from, to) && find(s) == find(e)) {
println(cost)
return
}
}
println(0)
}
fun find(x: Int): Int {
return if (x == parent[x]) x
else {
parent[x] = find(parent[x])
parent[x]
}
}
fun union(x: Int, y: Int): Boolean {
val (nx, ny) = find(x) to find(y)
return if (nx == ny) false
else {
parent[nx] = ny
true
}
}
코드 자체는 크루스칼 알고리즘 기반의 최소 스패닝 트리와 동일합니다.
크루스칼(분리 집합과 유니온 - 파인드 응용)에 대해서는 아래 포스팅을 참고해주세요.
https://uknowblog.tistory.com/61#article-3-2--union(x,y)
[자료구조] 분리 집합(Disjoint set)과 유니온 - 파인드(Union-Find)
분리집합? 분리집합이란 서로소 집합이라고도 불립니다. 이름에서도 알 수 있듯, 각각의 집합이 공통 원소를 가지지 않는 집합입니다. 즉 전체 집합 U에 두 개의 집합 A, B가 있을 때 A ∩ B = Ø 가
uknowblog.tistory.com
다만, 가중치를 기준으로 정렬할 때 내림차순(desc)으로 정렬한다는 점,
시작 노드와 도착 노드가 연결된 순간 (find(s) == find(e)) 답을 출력하고 프로그램을 종료한다는 점이 포인트입니다.
후기
최소 스패닝 트리를 이런 식으로도 사용할 수 있구나를 알게된 재밌었던 문제였습니다.
사실 접근방식 자체는 금방 떠올렸는데,
입력 전 혹은 후에 공백이 있는지... split 과정에서 NumberFormat 런타임 에러때문에 다소 시간을 잡아먹었던 문제였습니다.
저 같은 경우엔 입력을 받은 뒤 trim()으로 공백을 제거하여 해결하였습니다.,
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [백준 12869번] [Kotlin] 뮤탈리스크 (4) | 2023.11.10 |
|---|---|
| [백준 10838번] [Kotlin] 트리 (0) | 2023.11.08 |
| [백준 14868번] 문명 (0) | 2023.10.31 |
| [백준 2342번] [Kotlin] Dance Dance Revolution (1) | 2023.10.16 |
| [백준 17114번] [Kotlin] 하이퍼 토마토 (1) | 2023.10.10 |
