유클리드 기하학(Euclidean geometry)이란 무엇일까요?
고대 그리스 수학자 유클리드가 정립한 기하학으로,
우리가 초중고 수학시간에 배운 대부분의 기하학은 유클리드 기하학으로 보아도 됩니다.
오늘은 유클리드 기하학에서 사용되는 유클리드 거리와,
비 유클리드 기하학 중 택시 기하학의 맨해튼 거리에 알아보겠습니다.
1. 유클리드 거리

위 2차원 평면에서, 두 점의 거리는 어떻게 구할 수 있을까요?

매우 간단합니다. 피타고라스를 통해 손쉽게 구할 수 있습니다.
점 p(x1, y1)와 q(x2,y2)가 있을 때 이 둘 사이의 거리는 아래와 같습니다.

위와 같이 일반적인 평면에서 두 점 사이의 최단거리를 구한 것을
유클리드 거리라고 합니다.
일상 생활에서 일반적으로 사용하는 거리이죠.
<java />
int x1 = 2, y1 = 2;
int x2 = 6, y2 = 5;
double distance = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
System.out.println(distance);
// 출력
5
코드로 나타내면 위와 같습니다.
2. 맨해튼 거리
이번엔 위 유클리드 기하학이 아닌 비 유클리드 기하학.
그중에서도 조금 특별한 경우인 택시 기하학의 맨해튼 거리에 대해 알아보겠습니다.

맨해튼.
미국의 최대 도시이자 세계의 경제 중심지인 뉴욕에서도 중심부에 위치한 자치구입니다. 맨하탄이라고도 합니다.
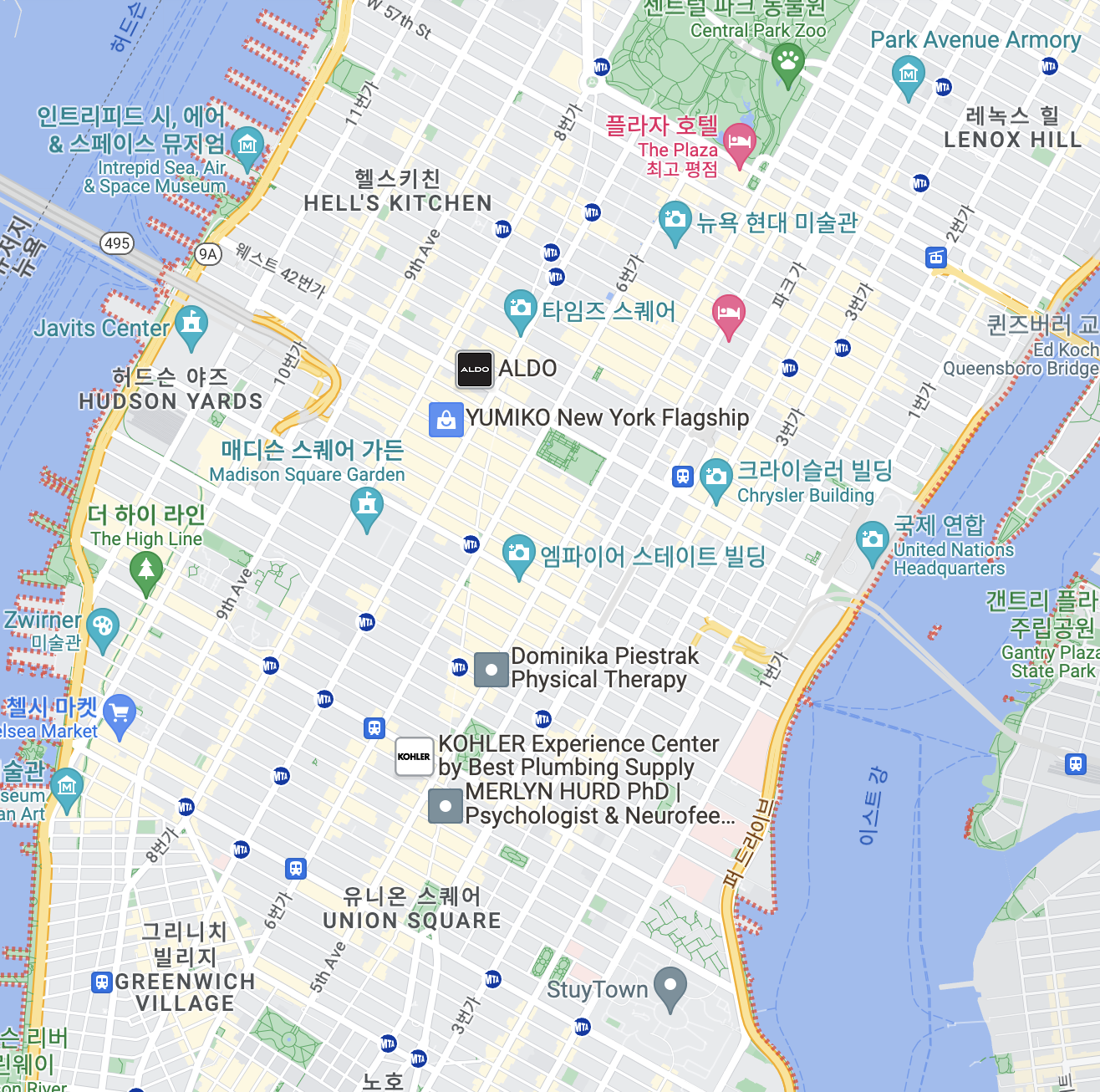
맨해튼의 도로를 보기 위해 구글 지도를 켜서 캡쳐해왔습니다.
조금의 공간낭비도 허용하지 않는 바둑판 모양의 도로가 인상적입니다.
격자무늬 도로를 가진 맨해튼에서 택시를 타고 이동해보겠습니다.
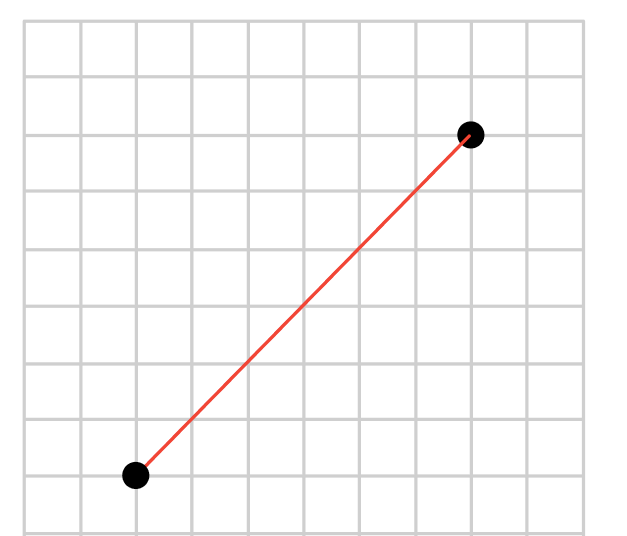
맨해튼의 한 지점에서 다른 한 지점으로 가기 위한 제일 빠른 방법은
유클리드 거리 처럼 바로 건물을 뚫고 일직선으로 가는 것입니다.
음... 안되겠죠?
아이언맨도 아니고 건물을 뚫고 갔다간 어마어마한 금액의 청구서가 날라올테니, 격자무늬의 도로를 이용해야 합니다.
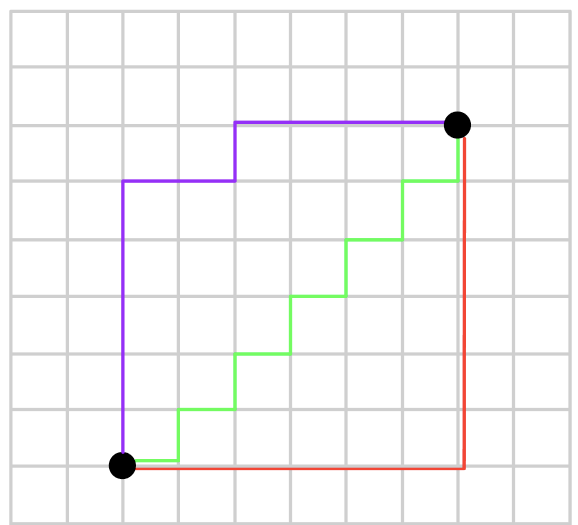
점과 점을 직선으로 이었던 유클리드 거리는 최단 경로가 단 하나였습니다.
하지만 격자무늬 도로를 이용했을 때, 최단 경로는 꽤나 많습니다.
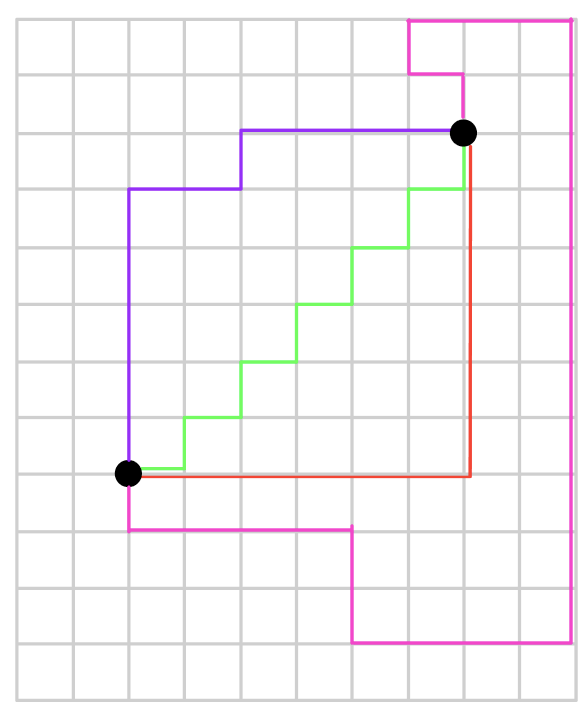
해당 목적지로 가는 방향의 도로를 타면, 도로를 어떻게 타던 한 지점에서 다른 한 지점으로 가는 거리는 모두 동일합니다.
보라색, 연두색, 빨간색 경로 모두 다 동일한 거리를 갖고 있죠.
이 경우 총 이동거리는 어떻게 될까요?
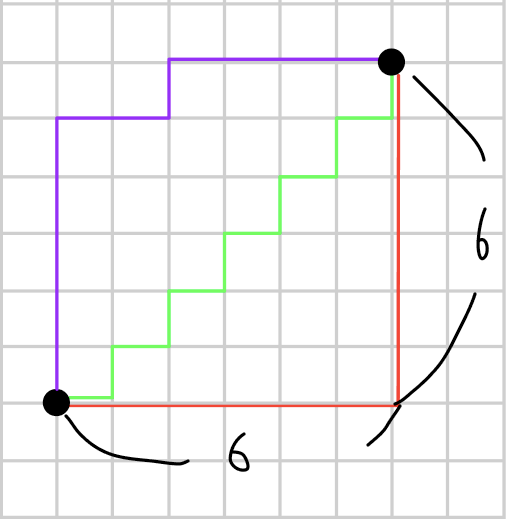
단지 세로로 이동한 거리 + 가로로 이동한 거리의 합인 12와 같습니다.
점 p(x1,y1)와 q(x2,y2)가 있을 때 이 둘 사이의 맨하탄 거리는 아래와 같습니다.
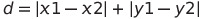
이를 코드로 나타내면 아래와 같습니다.
<java />
int x1 = 1, y1 = 2;
int x2 = 7, y2 = 8;
double distance = Math.abs(x1 - x2) + Math.abs(y1 - y2);
System.out.println(distance); // 12
물론 택시 기하학에서 택시 기사가 요금을 더 받기 위해
손님 몰래 '목적지 방향 외 도로'로 가는 경우는 고려하지 않습니다.
3. 후기
컴퓨터 공학을 배우다 보면 한 번쯤은 접하게 되는 맨해튼 거리 입니다.
맨해튼 거리를 처음 들었을 때, 해당 자료를 찾아보다가 비 유클리드 기하학이란 말에 다소 당황했지만,
개념 자체는 그리 어려운 게 아니였네요.
물론 깊게 들어가거나, 이 개념을 토대로 온갖 응용문제를 내다보면 지옥이 펼쳐질 수 있겠지만요.
비 유클리드 기하학을 보던 중 다른 비 유클리드 기하학들을 보게 되었는데,
이 글을 읽고 있는 당신이 수학과라면 건투를 빕니다...
'기타' 카테고리의 다른 글
| [Intellij 에러] error: unmappable character (0xE3) for encoding x-windows-949 에러 (0) | 2023.09.05 |
|---|---|
| 파이썬과 코틀린의 for문이 C, 자바의 for문과 다르게 생긴 이유 (feat. 부수효과(side-effect)) (0) | 2023.08.08 |
| x가 0이 아니면서 x와 -x가 같은 경우가 있을까? (백준 15549번) (0) | 2023.08.08 |
| 라이브러리와 프레임워크의 공통점과 차이점 (0) | 2023.08.04 |
| 노션 API를 사용해보자! (feat. 포스트맨) (0) | 2022.06.27 |

