https://www.acmicpc.net/problem/20302
20302번: 민트 초코
상원이가 고른 디저트가 “민트 초코”인 경우 mint chocolate, “치약”인 경우 toothpaste를 출력한다.
www.acmicpc.net
난이도 : 골드 4
태그 : 수학, 정수론, 소수판정, 에라토스테네스의채
설명
상당히 어려웠던 문제였습니다
그냥 단순히 입력으로 주어지는 연산을 그대로 했더니 당연하게 시간초과 발생하였고,


*, / 연산을 각각 리스트로 만들어
6 -> 2 * 3,
10 -> 2 * 5와 같이 소인수 분해 한 후, 각각에 리스트에 넣어준 뒤 (첫 항은 *로 처리),
* 연산이 남아있으면 유리수, / 연산이 남아있으면 유리수로 판단하였습니다.
6 / 4 = (3 * 2) / (2 * 2) = 3 / 2로, 나눗셈 연산이 단 한 항이라도 있다면
이는 정수가 아닌 유리수가 됩니다. (소숫점이 생긴다는 말)
그러나 이번에도 시간초과가 발생하였습니다.

간혹가다가, 자바/코틀린으로 풀면 시간초과가 발생하지만 C/C++로 작성하면 통과했던 적이 있었기에,
C++로 컨버팅하여 제출하여도 시간초과가 발생하였습니다. 언어가 아닌 제가 짠 코드가 문제였네요.


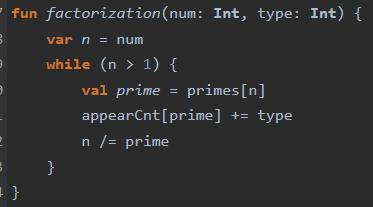
리스트를 써서 그런가? 하는 생각이 들어
리스트 대신 등장 횟수를 체크하는 배열을 하나 만들어놓고,
소인수분해 후 등장횟수를 *라면 +1 연산을, /라면 -1 연산을 하여,
-가 있으면 유리수, +가 있으면 유리수로 생각을 하였습니다.
리스트의 삭제 연산은 O(n)의 시간복잡도를 가지니,
배열 + 인덱스로 접근하여 시간복잡도 O(1)로 빠르게 연산할 수 있을 거라 생각 하였으나... 이번에도 시간초과.


소인수분해 과정을 브루트포스적으로 i부터 해당 수 까지 나눠 구하였는데, 아무래도 이게 문제라 생각하여,
각 수를 인수분해 할 수 있을 때, 몫을 미리 저장해놓고,
이를 소인수분해 할때 이용할 수 있지 않을까? 라는 생각에,
에라토스테네스의 채를 응용하여
각 수들을 소인수분해 할 수 있을 경우, 각 수들의 최소 몫들을 미리 저장해놨습니다.

많은 도전 끝에 마침내 통과하였습니다.
소스코드
import java.util.StringTokenizer
import kotlin.math.abs
val primes = IntArray(100002) { it }
val appearCnt = IntArray(100002) // 등장횟수 카운트
fun main() = with(System.`in`.bufferedReader()) {
val n = readLine().toInt()
for (i in 2 until primes.size) {
if (primes[i] == i) {
// 소인수분해 가능한 수는 미리 몫을 지정해놓음
// 에라토스테네스의 채 응용
for (j in i + i until primes.size step i) {
primes[j] = i
}
}
}
val st = StringTokenizer(readLine())
repeat(n) {
// 첫 번째 항은 *로 처리,
// *는 +, /는 -로 처리
val oper = if (it == 0 || st.nextToken() == "*") 1 else -1
var num = abs(st.nextToken().toInt()) // 중요한 것은 소숫점 포함 여부이므로, 부호는 날림
// 0이 곱해지면 무조건 정수가 됨
// 0으로 나뉘는 경우는 주어지지 않음 (문제조건)
if (num == 0) {
println("mint chocolate")
return@with
}
// 나눌 수 있는 몫을 미리 구해놓았으므로,
// 등장하는 수를 1 증가(*) 혹은 1 감소(/)
while (num > 1) {
val prime = primes[num]
appearCnt[prime] += oper
num /= prime
}
}
// 등장 횟수가 하나라도 음수가 있다면 이는 소숫점이 생긴다는 의미
for (i in 2..100001) {
if (appearCnt[i] < 0) {
println("toothpaste")
return@with
}
}
println("mint chocolate")
}
후기



2년 전에 처음 도전했다가, 실패하여 나중에 풀려고 납둔 문제였는데,
1년 전에 다시 도전했다가 또 실패하고, 결국 2년만에 풀었습니다.
파이썬 -> 자바 -> 코틀린 주 언어의 변화도 보이네요.
오랜 시간이 걸리긴 했지만 결국 통과했습니다.
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [구름톤 챌린지 19일차] [Kotlin] 대체 경로 (0) | 2023.09.08 |
|---|---|
| [구름톤 챌린지 18일차] [Kotlin] 중첩 점 (0) | 2023.09.07 |
| [백준 25585번] [Java, Kotlin] 86 ─에이티식스─ 1 (0) | 2023.08.16 |
| [백준 1331번] [Kotlin] 나이트 투어 (0) | 2023.08.04 |
| [백준 2563번] [Kotlin] 색종이 (0) | 2023.08.04 |

