https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 $-1$ 출력한다.
www.acmicpc.net
난이도 : 실버 3
태그 : 수학, 기하학, 많은 조건 분기
1. 설명
x1, y1과 반지롬
x2, y2와 반지름이 주어졌을 때,
위치의 개수를 출력하는 문제입니다.
즉, 외접하거나 내접하는 경우를 찾으면 되겠네요.
1.1. 위치의 개수가 무한대일 경우

두 원이 일치할 경우, 적이 있을 수 위치는 무한대입니다.
1.2. 위치의 개수가 0개일 경우

터렛의 두 사람의 위치가 같으나, 반지름이 다를 때,
두 원은 서로 교차하지 않습니다.
따라서 적이 있을 수 있는 위치의 경우의 수는 0개 입니다.
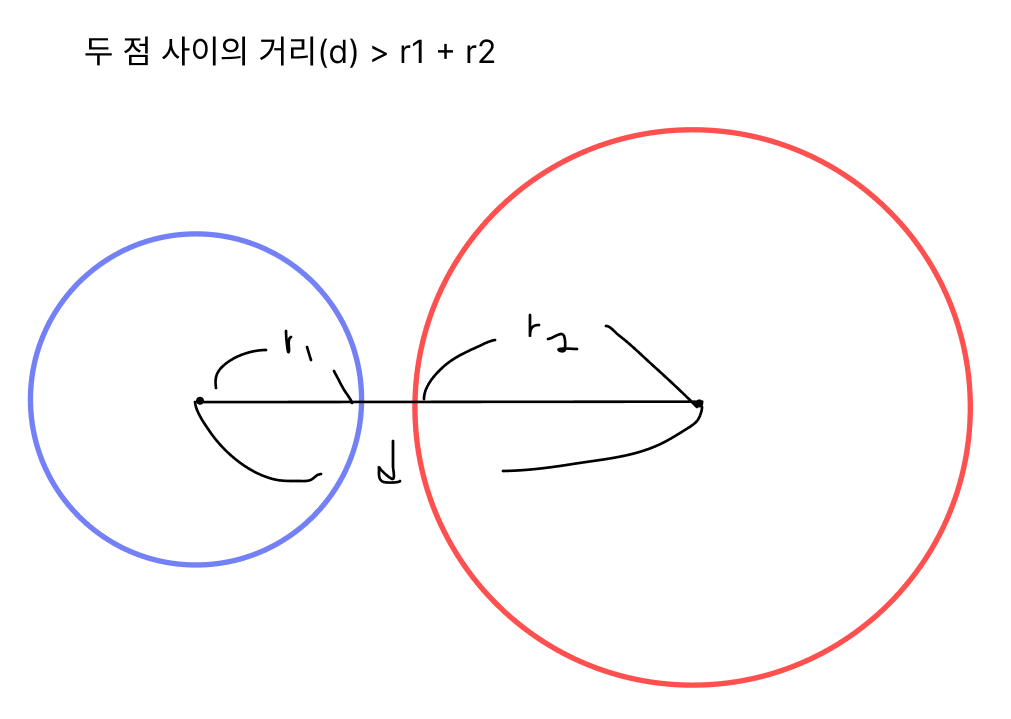
두 원의 중심이 서로 같지 않으면서,
두 원의 반지름의 합 보다 두 점 사이의 거리가 더 크다면,
두 원은 서로 접하지 않습니다. 따라서 적이 있을 수 있는 경우의 수는 0개 입니다.
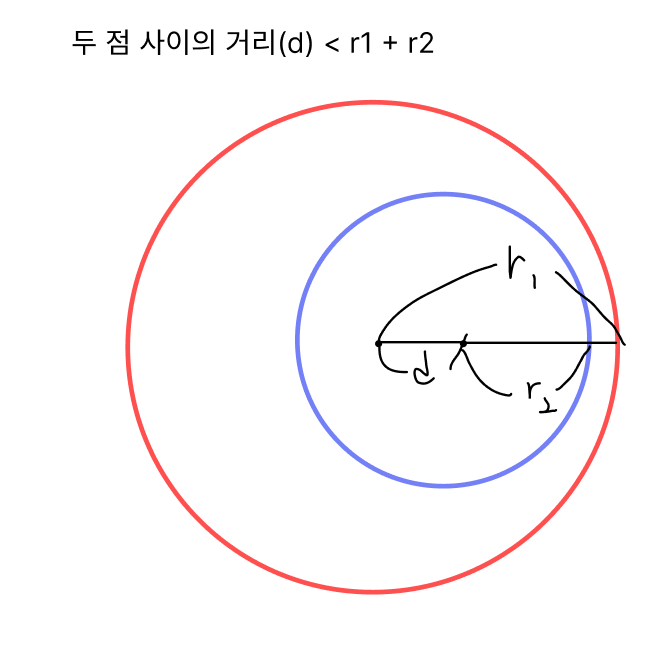
두 원의 중심이 서로 같지 않으면서,
두 원의 반지름의 합 보다 두 점 사이의 거리가 더 작다면,
두 원은 서로 접하지 않습니다. 따라서 적이 있을 수 있는 경우의 수는 0개 입니다.
1.3. 위치의 개수가 2개
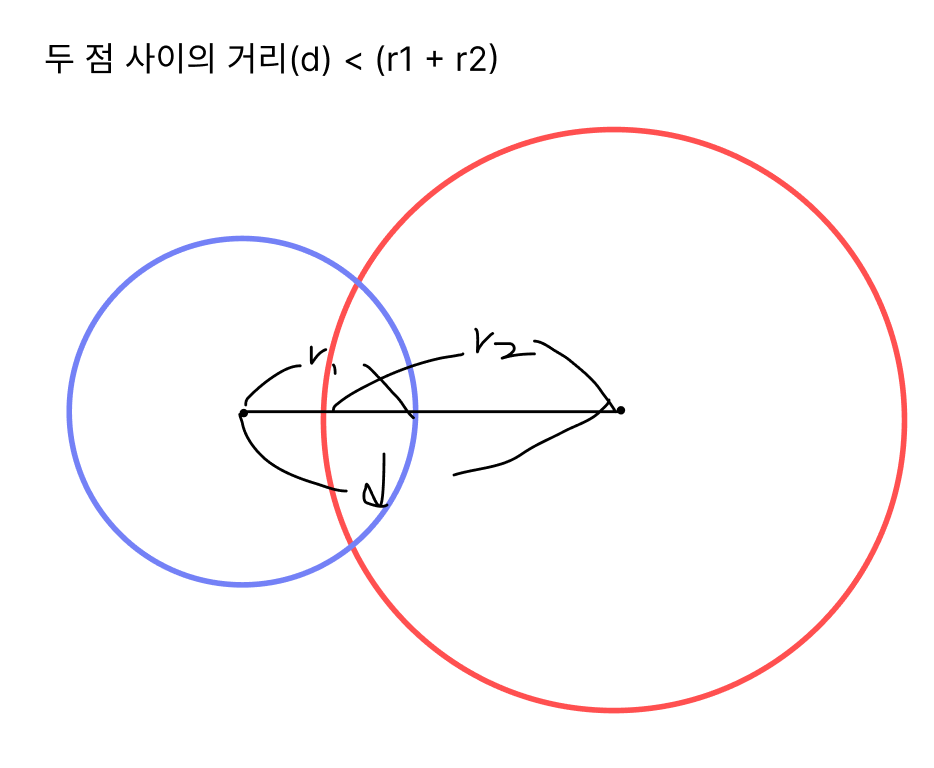
원의 중심이 서로 같지 않으면서,
각 원의 중심간의 거리가 d라 했을 때,
반지름 r1과 r2의 합이 d 보다 크다면
적이 있을 수 있는 위치는 2개 입니다.
1.4. 위치의 개수가 1개
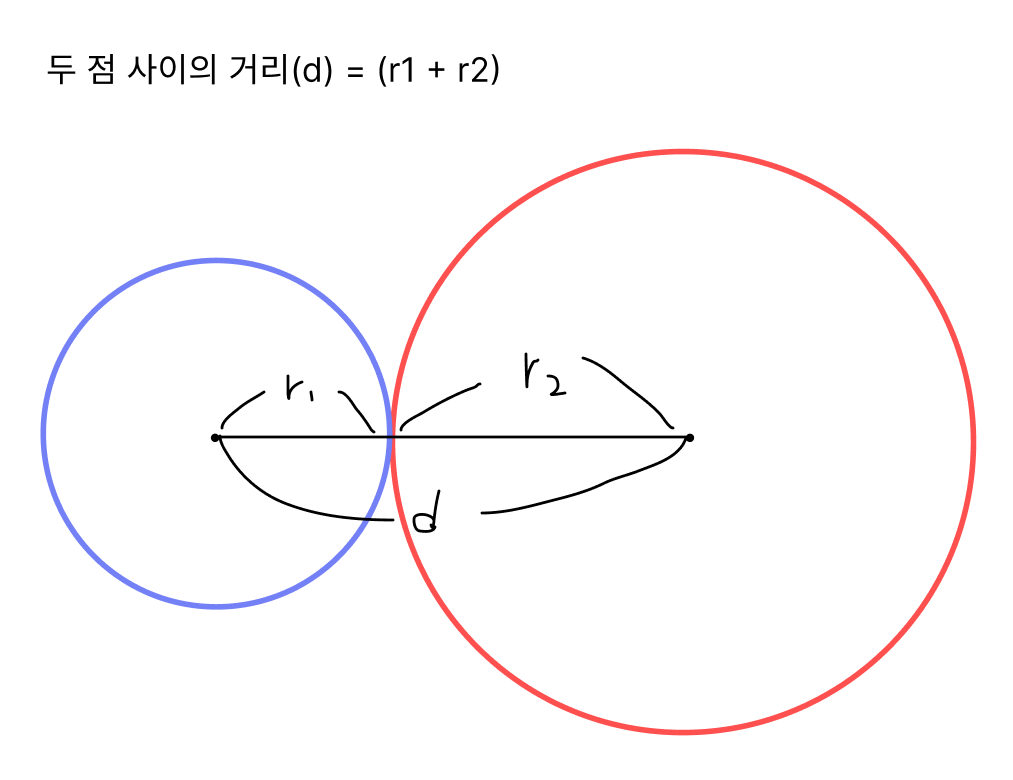
두 원의 중심이 서로 다르면서,
두 원의 중심 사이의 거리가 두 반지름의 합과 같다면
두 원은 서로 외접합니다.
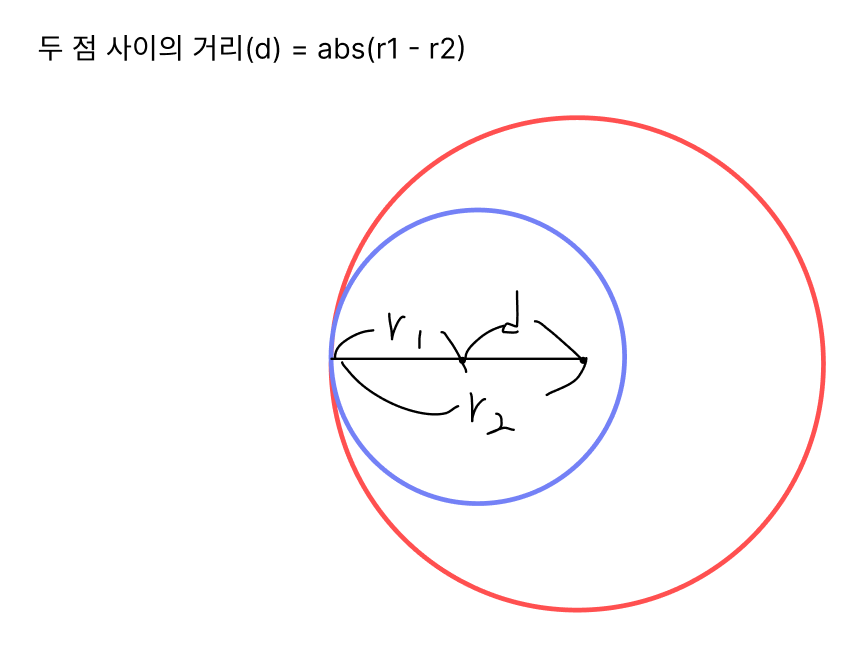
두 원의 중심이 서로 다르면서,
두 반지름의 차이가 두 점 사이의 거리와 같다면 이는 원이 내접함을 의미하빈다.
2. 소스코드
<python />
num = int(input())
a = list
for i in range(num):
a = list(map(int,input().split()))
d = (a[0] - a[3]) ** 2 + (a[1] - a[4]) ** 2
if a[0] == a[3] and a[1] == a[4] and a[2] == a[5]: #원의 좌표 일치, r 일치
print(-1)
elif a[0] == a[3] and a[1] == a[4] and a[2] != a[5]: #원의 좌표 일치, r 불일치
print(0)
elif d == (a[2] - a[5]) ** 2:
print(1)
elif d < (a[2]-a[5]) ** 2:
print(0)
elif d == (a[2]+a[5]) ** 2:
print(1)
elif d < (a[2]+a[5]) ** 2:
print(2)
elif d > (a[2]+a[5]) ** 2:
print(0)
3. 후기
꽤나 재밌었던 문제였습니다.
기하학 문제는 꽤 신기한게 많은 것 같네요.
'코딩테스트 > Python' 카테고리의 다른 글
| [백준 11022번] [Python] A + B - 8 (0) | 2023.04.17 |
|---|---|
| [백준 10952번] [Python] A + B - 5 (0) | 2023.04.17 |
| [백준 10951번] [Python] A+B - 4 (2) | 2023.04.17 |
| [백준 8958번] [Python] OX퀴즈 (0) | 2023.04.17 |
| [백준 2581번] [Python] 소수 (0) | 2023.03.30 |

