https://www.acmicpc.net/problem/2610
2610번: 회의준비
첫째 줄에 회의에 참석하는 사람의 수 N이 주어진다. 참석자들은 1부터 N까지의 자연수로 표현되며 회의에 참석하는 인원은 100 이하이다. 둘째 줄에는 서로 알고 있는 관계의 수 M이 주어진다. 이
www.acmicpc.net
난이도 : 골드 2
태그 : 그래프 이론, 자료 구조, 그래프 탐색, 분리 집합, 플로이드–워셜
설명
다소 복잡한 문제라, 지문을 두 세번 정도 정독했던 것 같네요.
서로 알고 있는 사람들의 관계가 주어질 때,
서로 알고 있을 경우 무조건 같은 위원회지만,
위원회는 최대한 많아야 하므로, 서로 알고 있지 않을 경우 무조건 다른 위원회로 분리합니다.

위의 말은 최댓값이... 최소가 된다...?는 말 때문에 처음에는 이해가 잘 안됬는데요.
저 같은 분들이 있을까봐 그림을 그려왔습니다.

위와 같이, 1번과 2번이 서로 아는 사이, 2번과 3번이 서로 아는 사이일 때 셋은 같은 위원회가 됩니다.

그럼, 1번이 대표가 되었을 경우, 3번이 대표인 1번에게 전달하려면 어떻게 해아 할까요?
3 -> 2 -> 1 방식으로 2번을 거쳐 대표에게 전달해야 합니다.
이는 3번이 대표가 되어도 마찬가지 입니다.
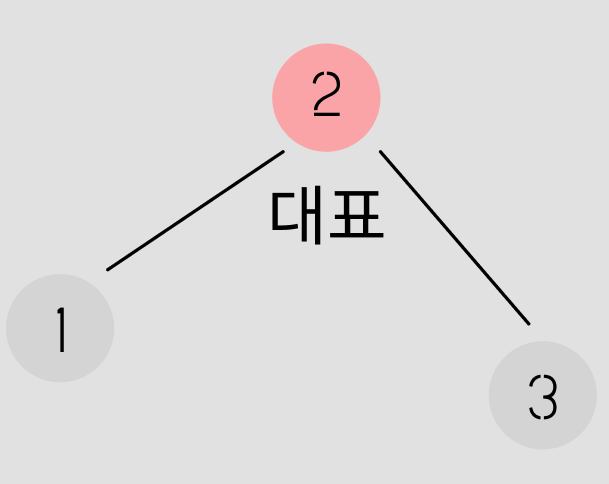
하지만, 2번이 대표가 되면?
1번, 3번 모두 대표에게 직접적으로 이야기를 전달할 수 있습니다.
즉 각 노드에서 가장 먼 노드를 찾되, 그 길이가 가장 짧은 경우를 찾는 것입니다.
그렇다면, 각 노드간의 거리는 어떻게 구할까요?
쉽게 구하기 위해 서로 인접한 노드의 거리를 1이라고 가정할 수 있겠습니다.
가장 먼저 떠오르는건 아무래도 DFS/BFS 입니다.
이 경우, 가장 먼 노드를 찾을 수 있지요. 혹은 다익스트라를 개조해 최장 경로를 찾을 수도 있을 것 같습니다.
하지만, 해당 문제 같은 경우, 한 노드에서 가장 먼 노드를 찾는 것이 아닌,
각 노드쌍에 대한 최장경로를 찾는 문제입니다.
노드쌍, 최장/최단 경로. 플로이드 와샬을 유용하게 쓸 수 있을 것 같습니다.
그렇다면, 서로 같은 위원회에 속해 있는지는 어떻게 알까요?
이 역시 분리집합, DFS/BFS 등 여러 방법이 있습니다.
하지만, 서로 인접한 노드간의 가중치를 1로 한 채 이미 플로이드 워셜을 돌려놓았습니다.
때문에, 갈 수 있는 경로가 없는 다른 위원회의 경우, 초기값 INF 그대로입니다.
즉, 갈 수 있는 경로가 있다면 모두 같은 위원회라는 것입니다.
때문에, 같은 파티에 있는 각 사람들 중, 가장 먼 노드쌍을 구하고, 그 길이가 최소가 되는 경우를 찾으면 됩니다.
이 아이디어를 소스코드로 옮겨보겠습니다.
소스코드
import java.util.StringTokenizer
fun main() = with(System.`in`.bufferedReader()) {
val INF = 987654321
val n = readLine().toInt()
val m = readLine().toInt()
val connect = Array(n + 1) { Array(n + 1) { INF } }
repeat(n) {
connect[it + 1][it + 1] = 0
}
repeat(m) {
val st = StringTokenizer(readLine())
val (a, b) = Array(2) { st.nextToken().toInt() }
connect[a][b] = 1
connect[b][a] = 1
}
// 플로아드 - 와샬 적용
for (k in 1..n) {
for (i in 1..n) {
for (j in 1..n) {
if (connect[i][j] > connect[i][k] + connect[k][j]) {
connect[i][j] = connect[i][k] + connect[k][j]
}
}
}
}
val visited = BooleanArray(n + 1)
val president = ArrayList<Int>()
for (i in 1..n) {
if (visited[i]) continue
val party = ArrayList<Int>()
for (j in 1..n) {
// i와 j로 가는 경로가 있다면 (!= INF) i는 j 와 같은 위원회!!!
if (connect[i][j] != INF) {
party.add(j)
visited[j] = true
}
}
var min = INF
var minIdx = 0
party.forEach { p ->
var max = 0
for (j in 1..n) {
// i와 j로 가는 경로가 있다면 (!= INF) i는 j 와 같은 위원회,
// 그 중에서 가장 멀리 있는 사람을 찾음
if (connect[p][j] != INF && connect[p][j] > max) {
max = connect[p][j]
}
}
// 가장 멀리 있는 사람 쌍 중에서 길이가 가장 짧은 쌍을 찾음
if (max < min) {
min = max
minIdx = p
}
}
president.add(minIdx)
}
val sb = StringBuilder()
sb.append(president.size).append("\n")
president.sorted().forEach {
sb.append("$it\n")
}
print(sb)
}
후기
처음에 같은 위원회에 속한지 어떻게 판단하지? 라는 생각에
분리집합을 응용하여 같은 파티에 속해있는지 판단하는 코드를 넣었다가,
어? 생각해보니까 다른 위원회는 가는 경로가 아예 없지 않나? 하는 생각에 다시 짜봤는데, 잘 작동하네요.
푸는데 거의 3시간 정도 걸렸던 것 같습니다...ㅠ 플로이드 워셜의 새로운 사용방법을 터득하고 가네요.
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [백준 18110번] [Kotlin] solved.ac (0) | 2023.06.14 |
|---|---|
| [백준 2696번] [Kotlin] 중앙값 구하기 (0) | 2023.06.13 |
| [백준 2615번] [Kotlin] 오목 (0) | 2023.06.11 |
| [백준 17136번] [Kotlin] 색종이 붙이기 (0) | 2023.06.10 |
| [백준 11000번] [Kotlin] 강의실 배정 (0) | 2023.06.05 |

