https://www.acmicpc.net/problem/2477
2477번: 참외밭
첫 번째 줄에 1m2의 넓이에 자라는 참외의 개수를 나타내는 양의 정수 K (1 ≤ K ≤ 20)가 주어진다. 참외밭을 나타내는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지
www.acmicpc.net
난이도 : 실버 2
태그 : 수학, 구현, 기하학
설명
실제 코딩테스트에 연습삼아 응시해봤다가, 기하학 문제에 큰 쓴맛을 느끼고, 기하학 문제를 공부하기로 마음 먹었습니다.
첫 번째 기하학 문제. 참외밭입니다.
밭은 항상 ㄱ 또는 ㄱ을 회전한 모양을 하고 있고, 이 육각형 임의의 점 중 하나에서 시작하여,
동서남북 방향과 길이가 주어집니다.
아, 큰 사각형에서 작은 사각형 그냥 빼면 되겠다. 를 생각하는데는 그리 오리 걸리지 않았으나,
작은 사각형의 넓이를 구하는게 생각보다 쉽지 않았습니다.
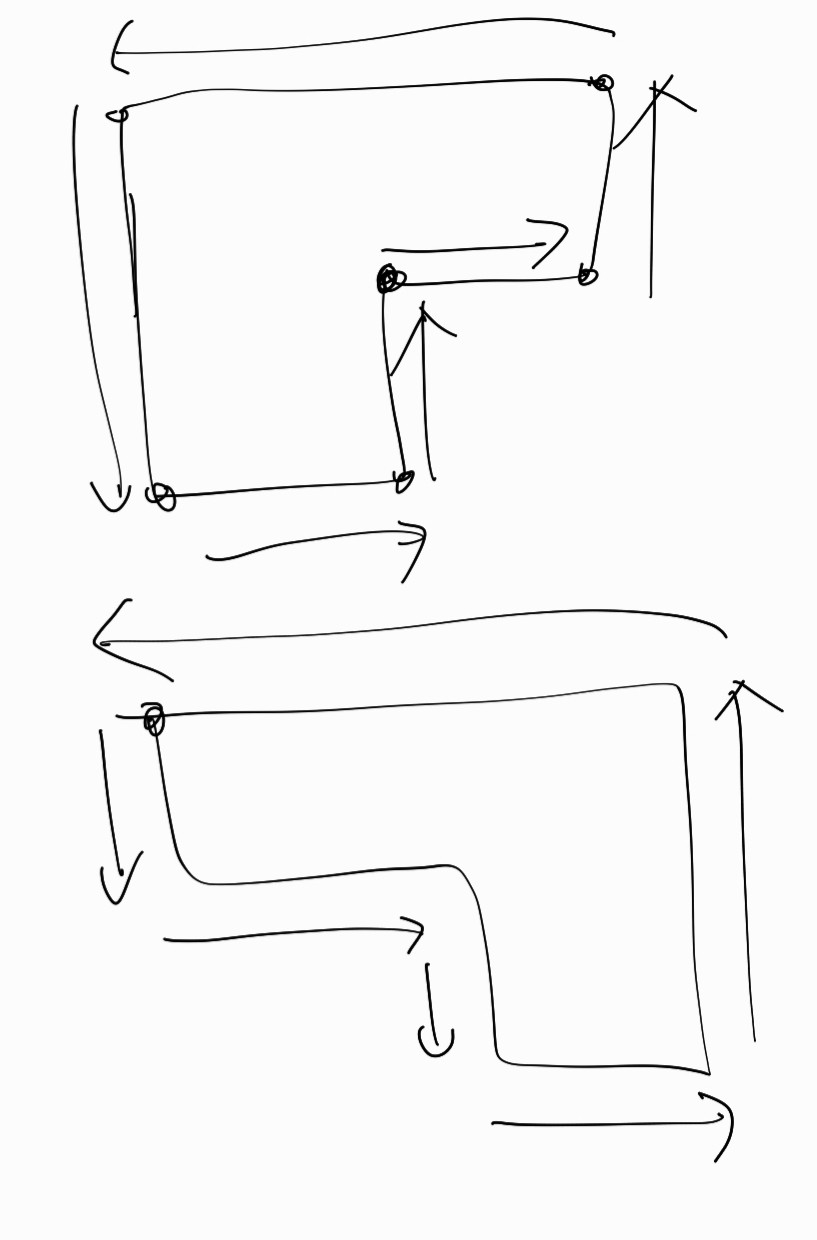
참외밭이 어떤 형태이든, 어느 방향부터 시작하든, 시계방향이든 반시계방향이든,
들어간 부분의 넓이는 같은 방향이 2번 연속 나옵니다.
반시계 방향이니, 남/동/남/동, 동/북/동/북 등으로 무조건 나오는 것이지요.
즉, 현재의 값과 2 이전의 값이 같고, 1 이전의 값과 3 이전의 값이 같으면 이는 들어간 부분의 길이라는 것입니다.
소스코드
fun main(): Unit = with(System.`in`.bufferedReader()) {
val n = readLine().toLong() // 참외 개수
val dirLen = Array(12) { Pair(0, 0) }
repeat(6) {
val (dir, len) = readLine().split(" ").map { it.toInt() }
dirLen[it] = Pair(dir, len)
dirLen[it + 6] = Pair(dir, len)
}
for (i in 3 until 12) {
if (dirLen[i].first == dirLen[i - 2].first && dirLen[i - 1].first == dirLen[i - 3].first) {
// 전체 넓이 = 전체 사각형 - 빈 넓이
println((dirLen[i + 1].second * dirLen[i + 2].second - dirLen[i - 2].second * dirLen[i - 1].second) * n)
break
}
}
}
저는 배열의 인덱스를 고려해 배열을 2배 크기로 잡아두고,
3부터 검사를 시작하였습니다.
이후, 큰 사각형에서 작은 사각형의 넓이를 빼서 참외밭의 넓이를 구한 뒤, n을 곱해 답을 출력합니다.
후기
기하 문제를 잘 풀어보지 않으니, 실버 2도 다소 어렵고 생소하네요.
좀 더 연습해야겠습니다.
'코딩테스트 > Kotlin' 카테고리의 다른 글
| [백준 2355번] [Kotlin] 시그마 (0) | 2023.03.11 |
|---|---|
| [백준 1264번] [Kotlin] 모음의 개수 (0) | 2023.03.11 |
| [백준 17281번] [Kotlin] ⚾ (0) | 2023.03.07 |
| [백준 18352번] [Kotlin] 특정 거리의 도시 찾기 (0) | 2023.02.27 |
| [백준 24309번] [Kotlin] РАВЕНСТВО (0) | 2023.02.22 |
